
分析 根据题意和等差数列的定义得:$\frac{{a}_{n+1}+λ}{{3}^{n+1}}-\frac{{a}_{n}+λ}{{3}^{n}}=d$,把递推公式代入化简后由整体思想求出λ的值.
解答 解:因为{$\frac{{{a_n}+λ}}{3^n}$}为等差数列,
所以$\frac{{a}_{n+1}+λ}{{3}^{n+1}}-\frac{{a}_{n}+λ}{{3}^{n}}=d$,d为常数,
因为an+1=3an+3n-8(n∈N+),
所以$\frac{{3a}_{n}+{3}^{n}-8+λ}{{3}^{n+1}}-\frac{{a}_{n}+λ}{{3}^{n}}=d$,
则左边=$\frac{{3a}_{n}+{3}^{n}-8+λ-(3{a}_{n}+3λ)}{{3}^{n+1}}$
=$\frac{{3}^{n}-8-2λ}{{3}^{n+1}}$=$\frac{1}{3}+\frac{-8-2λ}{{3}^{n+1}}$为常数,
则-8-2λ=0,解得λ=-4,
故答案为:-4.
点评 本题考查等差数列的定义,以及数列递推公式的应用,考查整体思想,化简、变形能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | p2 | B. | p2(1-p) | C. | ${C}_{3}^{2}$p2 | D. | ${C}_{3}^{2}$p2(1-p) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
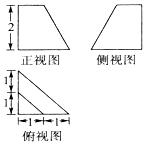
| A. | $\frac{7}{3}$ | B. | 7 | C. | 13 | D. | $\frac{{17+3\sqrt{10}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x1)=f(x2)=0,则x1-x2=kπ(k∈Z) | |
| B. | 函数f(x)的图象关于(-$\frac{π}{8}$,0)对称 | |
| C. | 函数f(x)的图象与g(x)=3cos(2x+$\frac{π}{4}$)的图象相同 | |
| D. | 函数f(x)在[-$\frac{1}{8}$π,$\frac{3}{8}$π]上递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,$\frac{2}{3}$) | B. | [0,$\frac{3}{4}$) | C. | ($\frac{3}{4}$,+∞) | D. | (0,$\frac{2}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
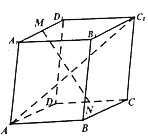 已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.
已知平行六面体ABCD-A1B1C1D1,设A1D1中点为M,CD的中点为N,若∠A1AD=∠A1AB=∠BAD=60°且AA1=AB=AD=1,则|AC1|=$\sqrt{6}$,若$\overrightarrow{MN}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{A{A}_{1}}$,则x+y+z=0.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com