练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列函数中，值域为(0，＋∞)的是(　　)

    A. y＝ B. y＝

    C. y＝ D. y＝x2＋1

    【答案】B

    【解析】y＝的值域为[0，＋∞)，y＝的值域为(－∞，0)∪(0，＋∞)，y＝x2＋1的值域为[1，＋∞),故选B.

    点睛:求函数的值域或最值的方法有很多,经常使用有以下几种:(1)换元法,把题目中出现多次的一个复杂的部分看作一个整体，通过简单的换元把复杂函数变为简单函数，使用换元法时，要特别注意换元后新元的范围（即定义域）;(2)分离常数法,求一次分式函数值域可用分离常数法;(3)判别式法,把函数转化成关于x的二次方程，通过方程有实数根，根据判别式，从而求得原函数的值域;(4)函数的单调性法,确定函数在定义域（或某个定义域的子集）上的单调性，借助单调性求出函数的值域.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司在迎新年晚会上举行抽奖活动，有甲、乙两个抽奖方案供员工选择；

    方案甲：员工最多有两次抽奖机会，每次抽奖的中奖率为.第一次抽奖，若未中奖，则抽奖结束.若中奖，则通过抛一枚质地均匀的硬币，决定是否继续进行第二次抽奖，规定：若抛出硬币，反面朝上，员工则获得500元奖金，不进行第二次抽奖；若正面朝上，员工则须进行第二次抽奖，且在第二次抽奖中，若中奖，获得奖金1000元；若未中奖，则所获奖金为0元.

    方案乙：员工连续三次抽奖，每次中奖率均为，每次中奖均可获奖金400元.

    （1）求某员工选择方案甲进行抽奖所获奖金（元）的分布列；

    （2）某员工选择方案乙与选择方案甲进行抽奖，试比较哪个方案更划算？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题12分）根据国家环保部新修订的《环境空气质量标准》规定：居民区PM2．5的年平均浓度不得超过35微克/立方米，PM2．5的24小时平均浓度不得超过75微克/立方米．某城市环保部门随机抽取了一居民区去年20天PM2．5的24小时平均浓度的监测数据，数据统计如下：

    ]

    组别

    PM2.5浓度（微克/立方米）

    频数（天）

    频率

    第一组

    3

    0.15

    第二组

    12

    0.6

    第三组

    3

    0.15

    第四组

    2

    0.1

    （Ⅰ）从样本中PM2．5的24小时平均浓度超过50微克/立方米的5天中，随机抽取2天，求恰好有一天PM2．5的24小时平均浓度超过75微克/立方米的概率；

    （Ⅱ）求样本平均数，并根据样本估计总体的思想，从PM2．5的年平均浓度考虑，判断该居民区的环境是否需要改进？说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数（，，，）的图象在点处的切线的斜率为，且函数为偶函数．若函数满足下列条件：①；②对一切实数，不等式恒成立．

    （1）求函数的表达式；

    （2）设函数（）的两个极值点，（）恰为的零点，当时，求的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某地上年度电价为0．8元，年用电量为1亿千瓦时．本年度计划将电价调至0．55元～0．75元之间，经测算，若电价调至元，则本年度新增用电量(亿千瓦时)与元成反比例．又当时，．

    （1）求与之间的函数关系式；

    （2）若每千瓦时电的成本价为0．3元，则电价调至多少时，本年度电力部门的收益将比上年增加20%？[收益用电量(实际电价－成本价)]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】宿州市教体局为了了解届高三毕业生学生情况，利用分层抽样抽取位学生数学学业水平测试成绩作调查，制作了成绩频率分布直方图，如图所示，其中成绩分组区间是：，，，，，.

    （Ⅰ）求图中的值；

    （Ⅱ）根据直方图估计宿州市届高三毕业生数学学业水平测试成绩的平均分；

    （Ⅲ）在抽取的人中，从成绩在和的学生中随机选取人，求这人成绩差别不超过分的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数．

    （1）若，求的单调区间；

    （2）若函数在处有极值，请证明：对任意时，都有．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】口袋中装有2个白球和n（n≥2，nN*）个红球．每次从袋中摸出2个球（每次摸球后把这2个球放回口袋中），若摸出的2个球颜色相同则为中奖，否则为不中奖．

    （I）用含n的代数式表示1次摸球中奖的概率；

    （Ⅱ）若n=3，求3次摸球中恰有1次中奖的概率；

    （III）记3次摸球中恰有1次中奖的概率为f（p），当f（p）取得最大值时，求n的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着移动互联网时代的到来，手机的使用非常普遍，“低头族”随处可见。某校为了解家长和教师对学生带手机进校园的态度，随机调查了100位家长和教师，得到情况如下表：

    教师

    家长

    反对

    40

    20

    支持

    20

    20

    （1）是否有95%以上的把握认为“带手机进校园与身份有关”，并说明理由；

    （2）把以上频率当概率，随机抽取3位教师，记其中反对学生带手机进校园的人数为X，求随机变量X的分布列和数学期望．

    附：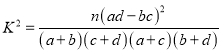

    P（K2≥k0）

    0.050

    0.010

    0.001

    k0

    3.841

    6.635

    10.828

    查看答案和解析>>

    同步练习册答案