
【题目】已知![]() .
.
(1)若![]() 在
在![]() 上单调递增,求
上单调递增,求![]() 的取值范围;
的取值范围;
(2)若![]() 有两个极值点
有两个极值点![]() ,
,![]() ,
,![]() ,证明:(i)
,证明:(i)![]() ;(ii)
;(ii)![]() .
.
【答案】(1)a≤6(2)见解析
【解析】
(1)f’(x)=4ex+2e-2x-a,转化为![]() ≥0求解,构造g(x)=4ex+2e-2x-a,求导求g(x)的最小值即可;(2)(ⅰ)由(1)设g(x)的两个零点为
≥0求解,构造g(x)=4ex+2e-2x-a,求导求g(x)的最小值即可;(2)(ⅰ)由(1)设g(x)的两个零点为![]() ,
,![]() ,
,![]() <0<
<0<![]() ,且a>6.令h(x)=g(x)-g(-x),证明h(x)在(0,+∞)上单调递减,当x>0时,h(x)<h(0)=0,进而证明g(
,且a>6.令h(x)=g(x)-g(-x),证明h(x)在(0,+∞)上单调递减,当x>0时,h(x)<h(0)=0,进而证明g(![]() )-g(-
)-g(-![]() )<0,从而g(
)<0,从而g(![]() )<g(-
)<g(-![]() ),,得
),,得![]() +
+![]() >0;(ⅱ)证明f(x)+f(-x)=-(ex+e-x-2)2+6≤6.可得f(
>0;(ⅱ)证明f(x)+f(-x)=-(ex+e-x-2)2+6≤6.可得f(![]() )<f(-
)<f(-![]() ),所以
),所以![]() <6.
<6.
(1)f’(x)=4ex+2e-2x-a,
令g(x)=4ex+2e-2x-a,则g’(x)=4ex-4e-2x,
显然g’(x)在(-∞,+∞)单调递增,且g(0)=0,
所以当x∈(-∞,0)时,g’(x)<0,g(x)单调递减;
当x∈(0,+∞)时,g’(x)>0,g(x)单调递增.
所以g(x)的最小值为g(0)=6-a,即f’(x)的最小值为6-a,
要使f(x)为单调增函数,则有f’(x)≥0,
所以6-a≥0,故a≤6.
(2)证明:
(ⅰ)由(1)得g(x)的两个零点为![]() ,
,![]() ,
,![]() <0<
<0<![]() ,且a>6.
,且a>6.
f(x)在(-∞,![]() )和(
)和(![]() ,+∞)上单调递增,在(
,+∞)上单调递增,在(![]() ,
,![]() )上单调递减.
)上单调递减.
令h(x)=g(x)-g(-x),
则h’(x)=g’(x)+g’(-x)
=4ex-4e-2x+4e-x-4e2x
=4[-(ex+e-x)2+(ex+e-x)+2]
=4[2-(ex+e-x
所以h(x)在(0,+∞)上单调递减,当x>0时,h(x)<h(0)=0.
所以g(![]() )-g(-
)-g(-![]() )<0,从而g(
)<0,从而g(![]() )<g(-
)<g(-![]() ),
),
又g![]() )=g(
)=g(![]() )=0,所以g(
)=0,所以g(![]() )<g(-
)<g(-![]() ),
),
因为g(x)在(-∞,0)上单调递减,![]() ,-
,-![]() ∈(-∞,0),
∈(-∞,0),
所以![]() >-
>-![]() ,故
,故![]() +
+![]() >0.
>0.
(ⅱ)f(x)+f(-x)=4ex-e-2x+4e-x-e2x=-(ex+e-x)2+4(ex+e-x)+2
=-(ex+e-x-2)2+6≤6.
由(ⅰ)得![]() +
+![]() >0,所以
>0,所以![]() >-
>-![]() >0,
>0,
由f(x)在(![]() ,
,![]() )上单调递减,可得f(
)上单调递减,可得f(![]() )<f(-
)<f(-![]() ),
),
从而有f(![]() )+f(
)+f(![]() )<f(
)<f(![]() )+f(-
)+f(-![]() )≤6,
)≤6,
所以f(![]() )+f(
)+f(![]() )<6.
)<6.


科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系中,以原点为极点,![]() 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线![]() :
:![]() ,过点
,过点![]() 的直线
的直线![]() 的参数方程为:
的参数方程为:![]() (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() 、
、![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)求线段![]() 的长和
的长和![]() 的积.
的积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆柱![]() 的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,
的一条母线,已知BC过底面圆的圆心O,D是圆O上不与点B、C重合的任意一点,![]()
![]()
![]() :
:
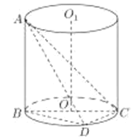
(1)求直线AC与平面ABD所成角的大小;
(2)求点B到平面ACD的距离;
(3)将四面体ABCD绕母线AB旋转一周,求由![]() 旋转而成的封闭几何体的体积;
旋转而成的封闭几何体的体积;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高速公路隧道设计为单向三车道,每条车道宽4米,要求通行车辆限高5米,隧道全长1.5千米,隧道的断面轮廓线近似地看成半个椭圆形状(如图所示).

(1)若最大拱高![]() 为6米,则隧道设计的拱宽
为6米,则隧道设计的拱宽![]() 至少是多少米?(结果取整数)
至少是多少米?(结果取整数)
(2)如何设计拱高![]() 和拱宽
和拱宽![]() ,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
,才能使半个椭圆形隧道的土方工程量最小?(结果取整数)
参考数据:![]() ,椭圆的面积公式为
,椭圆的面积公式为![]() ,其中
,其中![]() ,
,![]() 分别为椭圆的长半轴和短半轴长.
分别为椭圆的长半轴和短半轴长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在边长为8的菱形![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 折起,使点
折起,使点![]() 到达
到达![]() 的位置,且二面角
的位置,且二面角![]() 为
为![]() .
.
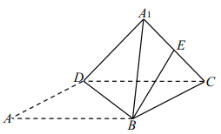
(1)求异面直线![]() 与
与![]() 所成角的大小;
所成角的大小;
(2)若点![]() 为
为![]() 中点,求直线
中点,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网络营销部门为了统计某市网友某日在某淘宝店的网购情况,随机抽查了该市当天![]() 名网友的网购金额情况,得到如下统计表(如图).
名网友的网购金额情况,得到如下统计表(如图).
网购金额(单位:千元) | 频数 | 频率 |
| 3 | 0.05 |
|
|
|
| 9 | 0.15 |
| 15 | 0.25 |
| 18 | 0.30 |
|
|
|

若网购金额超过![]() 千元的顾客定义为“网购达人”,网购金额不超过
千元的顾客定义为“网购达人”,网购金额不超过![]() 千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为
千元的顾客定义为“非网购达人”,已知“非网购达人”与“网购达人”人数比恰好为![]() .
.
(Ⅰ)试确定![]() 的值,并补全频率分布直方图(如图);
的值,并补全频率分布直方图(如图);
(Ⅱ)该营销部门为了进一步了解这![]() 名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取
名网友的购物体验,从“非网购达人”与“网购达人”中用分层抽样的方法抽取![]() 人,若需从这
人,若需从这![]() 人中随机选取
人中随机选取![]() 人进行问卷调查.设
人进行问卷调查.设![]() 为选取的
为选取的![]() 人中“网购达人”的人数,求
人中“网购达人”的人数,求![]() 的分布列及其数学期望.
的分布列及其数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线E:![]() 焦点F,过点F且斜率为2的直线与抛物线交于A、B两点,且
焦点F,过点F且斜率为2的直线与抛物线交于A、B两点,且![]() .
.
(1)求抛物线E的方程;
(2)设O是坐标原点,P,Q是抛物线E上分别位于x轴两侧的两个动点,且![]()
①证明:直线PQ必过定点,并求出定点G的坐标;
②过G作PQ的垂线交抛物线于C,D两点,求四边形PCQD面积的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com