
【题目】李先生家住![]() 小区,他工作在
小区,他工作在![]() 科技园区,从家开车到公司上班路上有
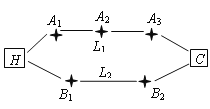
科技园区,从家开车到公司上班路上有![]() 两条路线(如图),
两条路线(如图),![]() 路线上有
路线上有![]() 三个路口,各路口遇到红灯的概率均为
三个路口,各路口遇到红灯的概率均为![]() ;
;![]() 路线上有
路线上有![]() 两个路口,各路口遇到红灯的概率依次为
两个路口,各路口遇到红灯的概率依次为![]() .
.
(Ⅰ)若走![]() 路线,求最多遇到1次红灯的概率;
路线,求最多遇到1次红灯的概率;
(Ⅱ)若走![]() 路线,求遇到红灯次数
路线,求遇到红灯次数![]() 的数学期望;
的数学期望;
(Ⅲ)按照“平均遇到红灯次数最少”的要求,请你帮助李先生从上述两条路线中选择一条最好的上班路线,并说明理由.
【答案】(1)![]() (2)
(2)![]() (3)选择
(3)选择![]() 路线上班最好.
路线上班最好.
【解析】
【试题分析】(1)走线路![]() 相当于
相当于![]() 次独立重复试验,按照二项分布的计算公式,计算恰好发生
次独立重复试验,按照二项分布的计算公式,计算恰好发生![]() 次和恰好发生
次和恰好发生![]() 次的概率,相加即可.(2)走线路
次的概率,相加即可.(2)走线路![]() ,则遇到红灯次数
,则遇到红灯次数![]() 的可能取值为
的可能取值为![]() ,按照独立事件概率计算公式计算对应的概率,写出并求其期望.(3)
,按照独立事件概率计算公式计算对应的概率,写出并求其期望.(3)![]() 线路是二项分布,利用公式
线路是二项分布,利用公式![]() 计算出期望,由于
计算出期望,由于![]() 的期望小,故选线路
的期望小,故选线路![]() .
.
【试题解析】
(Ⅰ)设“走![]() 路线最多遇到1次红灯”为事件
路线最多遇到1次红灯”为事件![]() ,
,
则 ![]() ,
,
所以走![]() 路线,最多遇到1次红灯的概率为
路线,最多遇到1次红灯的概率为![]() .
.
(Ⅱ)依题意,![]() 的可能取值为0,1,2.
的可能取值为0,1,2.
![]()
![]()
![]() .
.
随机变量![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 |
|
|
|
|
所以![]() .
.
(Ⅲ)设选择![]() 路线遇到红灯次数为
路线遇到红灯次数为![]() ,随机变量
,随机变量![]() 服从二项分布
服从二项分布![]() ~
~![]() ,所以
,所以![]() . 因为
. 因为![]() ,所以选择
,所以选择![]() 路线上班最好.
路线上班最好.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,把满足条件
,把满足条件![]() (对任意的
(对任意的![]() )的所有数列
)的所有数列![]() 构成的集合记为
构成的集合记为![]() .
.
(1)若数列![]() 的通项为
的通项为![]() ,判断
,判断![]() 是否属于
是否属于![]() ,并说明理由;
,并说明理由;
(2)若数列![]() 的通项为
的通项为![]() ,判断
,判断![]() 是否属于
是否属于![]() ,并说明理由;
,并说明理由;
(3)若数列![]() 是等差数列,且
是等差数列,且![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点P与点![]() 的距离比它到直线
的距离比它到直线![]() 的距离小1.
的距离小1.
(1)求动点P的轨迹C的方程;
(2)设P为直线![]() 上任一点,过点P作曲线C的切线
上任一点,过点P作曲线C的切线![]() ,
,![]() ,切点分别为A,B,直线
,切点分别为A,B,直线![]() ,
,![]() 与y轴分别交于M,N两点,点
与y轴分别交于M,N两点,点![]() 、
、![]() 的纵坐标分别为m,n,求证:m与n的乘积为定值.
的纵坐标分别为m,n,求证:m与n的乘积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() ,
,![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,已知曲线
轴正半轴为极轴建立极坐标系,已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,点
,点![]() 为
为![]() 上的动点,
上的动点,![]() 为
为![]() 的中点.
的中点.
(1)请求出![]() 点轨迹
点轨迹![]() 的直角坐标方程;
的直角坐标方程;
(2)设点![]() 的极坐标为
的极坐标为![]() 若直线
若直线![]() 经过点
经过点![]() 且与曲线
且与曲线![]() 交于点
交于点![]() ,弦
,弦![]() 的中点为
的中点为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了比较两种治疗某病毒的药(分别称为甲药,乙药)的疗效,某医疗团队随机地选取了服用甲药的患者和服用乙药的患者进行研究,根据研究的数据,绘制了如图1等高条形图
.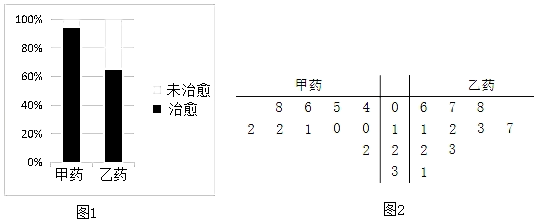
(1)根据等高条形图,判断哪一种药的治愈率更高,不用说明理由;
(2)为了进一步研究两种药的疗效,从服用甲药的治愈患者和服用乙药的治愈患者中,分别抽取了10名,记录他们的治疗时间(单位:天),统计并绘制了如图2茎叶图,从茎叶图看,哪一种药的疗效更好,并说明理由;
(3)标准差s除了可以用来刻画一组数据的离散程度外,还可以刻画每个数据偏离平均水平的程度,如果出现了治疗时间在(![]() 3s,
3s,![]() 3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
3s)之外的患者,就认为病毒有可能发生了变异,需要对该患者进行进一步检查,若某服用甲药的患者已经治疗了26天还未痊愈,请结合(2)中甲药的数据,判断是否应该对该患者进行进一步检查?
参考公式:s![]() ,
,
参考数据:![]() 48.
48.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在正六棱锥![]() 中,底面边长和侧棱分别是2和4,
中,底面边长和侧棱分别是2和4,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点,给出下面三个判断:(1)
的中点,给出下面三个判断:(1)![]() 和
和![]() 所成的角的余弦值为
所成的角的余弦值为![]() ;(2)
;(2)![]() 和底面所成的角是
和底面所成的角是![]() ;(3)平面
;(3)平面![]() 平面
平面![]() ;其中判断正确的个数是( )
;其中判断正确的个数是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着生活水平的逐步提高,人们对文娱活动的需求与日俱增,其中观看电视就是一种老少皆宜的娱乐活动.但是我们在观看电视娱乐身心的同时,也要注意把握好观看时间,近期研究显示,一项久坐的生活指标——看电视时间,是导致视力下降的重要因素,即看电视时间越长,视力下降的风险越大.研究者在某小区统计了每天看电视时间![]() (单位:小时)与视力下降人数
(单位:小时)与视力下降人数![]() 的相关数据如下:
的相关数据如下:
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
(1)请根据上面的数据求![]() 关于
关于![]() 的线性回归方程
的线性回归方程
(2)我们用(1)问求出的线性回归方程![]() 的
的![]() 估计回归方程
估计回归方程![]() ,由于随机误差
,由于随机误差![]() ,所以
,所以![]() 是
是![]() 的估计值,
的估计值,![]() 成为点(
成为点(![]() ,
,![]() )的残差.
)的残差.
①填写下面的残差表,并绘制残差图;
编号 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1.5 | 2 | 2.5 | 3 |
| 12 | 16 | 22 | 24 | 26 |
|
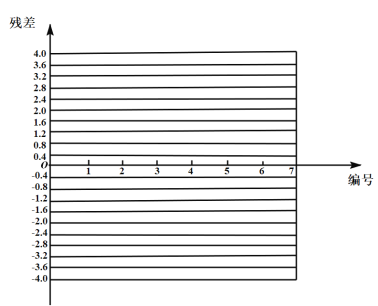
②若残差图所在带状区域宽度不超过4,我们则认为该模型拟合精度比较高,回归方程的预报精度较高,试根据①绘制的残差图分折该模型拟合精度是否比较高?
附:回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为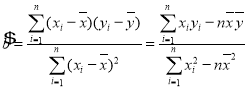 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以原点为极点,![]() 轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线
轴非负半轴为极轴,长度单位相同,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,直线
,直线![]() 过点
过点![]() ,倾斜角为
,倾斜角为![]() .
.
(1)将曲线![]() 的极坐标方程化为直角坐标方程,写出直线
的极坐标方程化为直角坐标方程,写出直线![]() 的参数方程的标准形式;
的参数方程的标准形式;
(2)已知直线![]() 交曲线
交曲线![]() 于
于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com