Question

【题目】已知椭圆C：9x2+y2=m2（m＞0），直线l不过原点O且不平行于坐标轴，l与C有两个交点A，B，线段AB的中点为M．
（1）证明：直线OM的斜率与l的斜率的乘积为定值；
（2）若l过点（ ，m），延长线段OM与C交于点P，四边形OAPB能否为平行四边形？若能，求此时l的斜率；若不能，说明理由．

Answer 1

【答案】
（1）证明：设直线l：y=kx+b，（k≠0，b≠0），A（x1，y1），B（x2，y2），M（xM，yM），

将y=kx+b代入9x2+y2=m2（m＞0），得（k2+9）x2+2kbx+b2﹣m2=0，

则判别式△=4k2b2﹣4（k2+9）（b2﹣m2）＞0，

则x1+x2= ，则xM= = ，yM=kxM+b= ，

于是直线OM的斜率kOM= = ，

即kOMk=﹣9，

∴直线OM的斜率与l的斜率的乘积为定值．

（2）解：四边形OAPB能为平行四边形．

∵直线l过点（ ，m），

∴由判别式△=4k2b2﹣4（k2+9）（b2﹣m2）＞0，

即k2m2＞9b2﹣9m2，

∵b=m﹣ m，

∴k2m2＞9（m﹣ m）2﹣9m2，

即k2＞k2﹣6k，

则k＞0，

∴l不过原点且与C有两个交点的充要条件是k＞0，k≠3，

由（1）知OM的方程为y= x，

设P的横坐标为xP，

由 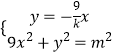得 ，即xP= ，

将点（ ，m）的坐标代入l的方程得b= ，

即l的方程为y=kx+ ，

将y= x，代入y=kx+ ，

得kx+ = x

解得xM= ，

四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分，即xP=2xM，

于是 =2× ，

解得k1=4﹣ 或k2=4+ ，

∵ki＞0，ki≠3，i=1，2，

∴当l的斜率为4﹣ 或4+ 时，四边形OAPB能为平行四边形．

【解析】（1）联立直线方程和椭圆方程，求出对应的直线斜率即可得到结论．（2）四边形OAPB为平行四边形当且仅当线段AB与线段OP互相平分，即xP=2xM ， 建立方程关系即可得到结论．
【考点精析】通过灵活运用直线的斜率，掌握一条直线的倾斜角α(α≠90°)的正切值叫做这条直线的斜率,斜率常用小写字母k表示,也就是 k = tanα即可以解答此题．