
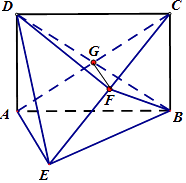
【题目】如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点 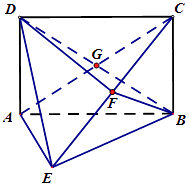
(1)求证:AE∥平面BFD
(2)求证:AE⊥平面BCE
(3)求三棱柱C﹣BGF的体积.
【答案】
(1)证明:依题意可知:G是AC中点,
∵BF⊥平面ACE,则CE⊥BF,而BC=BE,∴F是EC中点.
在△ABC中,FG∥AE,∴AE∥平面BFD
(2)证明:∵AD⊥平面ABE,AD∥BC,
∴BC⊥平面ABE,则AE⊥BC.
又∵BF⊥平面ACE,则CE⊥BF,
∴AE⊥平面BCE
(3)∵AE∥平面BFD,∴AE∥FG,而AE⊥平面BCG,
∴FG⊥平面BCE,∴GF⊥平面BCF.
∵G是AC的中点,∴F是CE的中点,且FG= ![]() ,
,
∵BF⊥平面ACE,∴BF⊥CE.
∴在Rt△BCE中,BF=CF= ![]() .
.
∴ ![]() ,
,
则 ![]() .
.
【解析】(1)依题意可知G是AC中点,由BF⊥平面ACE,得CE⊥BF,再由BC=BE,可得F是EC中点,得到FG∥AE,由线面平行的判定得AE∥平面BFD.(2)由AD⊥平面ABE,AD∥BC,可得BC⊥平面ABE,进一步得到AE⊥BC.结合BF⊥平面ACE,得CE⊥BF,由线面垂直的判定得AE⊥平面BCE;(3)由已知可得GF⊥平面BCF.解直角三角形求得△BCF的面积,然后利用等积法求得三棱柱C﹣BGF的体积.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案科目:高中数学 来源: 题型:
【题目】下面给出四个命题的表述: ①直线(3+m)x+4y﹣3+3m=0(m∈R)恒过定点(﹣3,3);
②线段AB的端点B的坐标是(3,4),A在圆x2+y2=4上运动,则线段AB的中点M的轨迹方程 ![]() +(y﹣2)2=1
+(y﹣2)2=1
③已知M={(x,y)|y= ![]() },N={(x,y)|y=x+b},若M∩N≠,则b∈[﹣
},N={(x,y)|y=x+b},若M∩N≠,则b∈[﹣ ![]() ,
, ![]() ];
];
④已知圆C:(x﹣b)2+(y﹣c)2=a2(a>0,b>0,c>0)与x轴相交,与y轴相离,则直线ax+by+c=0与直线x+y+1=0的交点在第二象限.
其中表述正确的是( (填上所有正确结论对应的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调增区间;
的单调增区间;
(2)设函数![]() ,
, ![]() .若函数
.若函数![]() 的最小值是
的最小值是![]() ,求
,求![]() 的值;
的值;
(3)若函数![]() ,
, ![]() 的定义域都是
的定义域都是![]() ,对于函数
,对于函数![]() 的图象上的任意一点
的图象上的任意一点![]() ,在函数
,在函数![]() 的图象上都存在一点
的图象上都存在一点![]() ,使得
,使得![]() ,其中
,其中![]() 是自然对数的底数,
是自然对数的底数, ![]() 为坐标原点.求
为坐标原点.求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
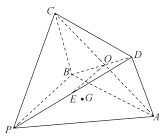
【题目】如图所示的几何体![]() 中,四边形
中,四边形![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点,
的中点, ![]() 为平面
为平面![]() 内任一点.
内任一点.
(1)在平面![]() 内,过
内,过![]() 点是否存在直线
点是否存在直线![]() 使
使![]() ?如果不存在,请说明理由,如果存在,请说明作法;
?如果不存在,请说明理由,如果存在,请说明作法;
(2)过![]() ,
, ![]() ,
, ![]() 三点的平面将几何体
三点的平面将几何体![]() 截去三棱锥
截去三棱锥![]() ,求剩余几何体
,求剩余几何体![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() ,抛物线
,抛物线![]() ,
, ![]() 与
与![]() 有公共的焦点
有公共的焦点![]() ,
, ![]() 与
与![]() 在第一象限的公共点为
在第一象限的公共点为![]() ,直线
,直线![]() 的倾斜角为
的倾斜角为![]() ,且
,且![]() ,则关于双曲线的离心率的说法正确的是()
,则关于双曲线的离心率的说法正确的是()
A. 仅有两个不同的离心率![]() 且
且![]() B. 仅有两个不同的离心率
B. 仅有两个不同的离心率![]() 且
且![]() C. 仅有一个离心率
C. 仅有一个离心率![]() 且
且![]() D. 仅有一个离心率
D. 仅有一个离心率![]() 且
且![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com