
����Ŀ��������ƽ��������ɵļ��ϼ���![]() ��
��![]() �Ǵ�
�Ǵ�![]() ��
��![]() �Ķ�Ӧ��ϵ������
�Ķ�Ӧ��ϵ������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ��
��![]() ����ʵ���������Ӧ��ϵ
����ʵ���������Ӧ��ϵ![]() ��ģΪ����
��ģΪ����![]() ��������
��������![]() �����ֵ����
�����ֵ����![]() �������ڷ�������
�������ڷ�������![]() ����ʵ��
����ʵ��![]() ʹ��
ʹ��![]() �����
�����![]() Ϊ
Ϊ![]() ��һ������ֵ��
��һ������ֵ��
��1����![]() ����
����![]() ��
��
��2�����![]() ������
������![]() ������ֵ��������Ӧ��
������ֵ��������Ӧ��![]() ��
��
��3����![]() ��Ҫʹ
��Ҫʹ![]() ��Ψһ������ֵ��ʵ��
��Ψһ������ֵ��ʵ��![]() ��
��![]() ��
��![]() ��
��![]() Ӧ����ʲô���������ҳ�һ����Ӧ��ϵ
Ӧ����ʲô���������ҳ�һ����Ӧ��ϵ![]() ��ͬʱ����������������������Ψһ������ֵ
��ͬʱ����������������������Ψһ������ֵ![]() ����
����![]() ������֤
������֤![]() ��������������.
��������������.
���𰸡�(1) ![]() ��(2) ��
��(2) ��![]() ʱ,
ʱ,![]() ;��
;��![]() ʱ,
ʱ, ![]() .����
.����![]() ��
��![]() ��(3)
��(3) ![]() ,֤��������
,֤��������
��������
(1)���¶����![]() ,������
,������![]() ��
��![]() ����.
����.
(2)������ֵ�Ķ���ɵ�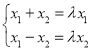 ,�ɴ˿ɵ�
,�ɴ˿ɵ�![]() ������ֵ,����Ӧ��
������ֵ,����Ӧ��![]()
(3) �ⷽ����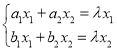 ,������ƽ�������ķ������֤������.
,������ƽ�������ķ������֤������.
(1)���ڴ�ʱ![]() ,����Ϊ����
,��������![]() ��������,��
��������,��![]() ,��
,��![]() ʱȡ���ֵ,���Դ�ʱ��
ʱȡ���ֵ,���Դ�ʱ��![]() ;
;
(2)��![]() ,�ɵã�
,�ɵã�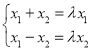 ,
,
��˷�����ɵã�![]() ,�Ӷ�
,�Ӷ�![]() .
.
��![]() ʱ,�ⷽ����
ʱ,�ⷽ����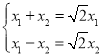 ,��ʱ������������ͬһ������,���Դ�ʱ��������������,Ϊ
,��ʱ������������ͬһ������,���Դ�ʱ��������������,Ϊ![]() (д��һ������),����
(д��һ������),����![]() ��
��![]() .
.
��![]() ʱ,ͬ���ɵ�,��Ӧ��
ʱ,ͬ���ɵ�,��Ӧ��![]() (д��һ������),����
(д��һ������),����![]() ��
��![]() (3)�ⷽ����
(3)�ⷽ����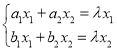 ,�ɵ�
,�ɵ�![]() �Ӷ�����
�Ӷ�����![]() ��
��![]() ƽ��,�Ӷ���
ƽ��,�Ӷ���![]() ��
��![]() ��
��![]() ��
��![]() Ӧ���㣺
Ӧ���㣺![]() .
.
��![]() ʱ,
ʱ,![]() ��Ψһ������ֵ,��
��Ψһ������ֵ,��![]() .����֤��Ϊ��
.����֤��Ϊ��
��![]() �Ķ����֪��
�Ķ����֪��![]() ,����
,����![]() Ϊ����ֵ.
Ϊ����ֵ.
��ʱ![]() ���㣺
���㣺![]() ,������Ψһ������ֵ.
,������Ψһ������ֵ.
��![]() ��������
��������![]() ,�Ӷ���
,�Ӷ���![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ�������п��Ժ���ѧ��ʦ�Ա���ȫ��ѧ������ѧ�ɼ���1��20���зֲ�����������ȡ��20��ѧ���ijɼ�Ϊ�������ɼ��þ�Ҷͼ��¼��ͼ��ʾ�����������ݲ�С�Ķ�ʧ��ͬʱ�õ����±���ʾ��Ƶ�ʷֲ�����
�����Σ��֣� |
|
|
|
|
| �ܼ� |
Ƶ�� |
| |||||
Ƶ�� |
| 0.25 |
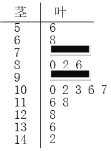
��1�������![]() ��
��![]() ��ֵ���ɼ���
��ֵ���ɼ���![]()
![]() ��Χ�ڵ���������
��Χ�ڵ���������
��2���ӳɼ�![]() �ڵ������������ȡ4�������������гɼ���
�ڵ������������ȡ4�������������гɼ���![]() �ڵ���������Ϊ�������
�ڵ���������Ϊ�������![]() ����
����![]() �ķֲ��м���ѧ����
�ķֲ��м���ѧ����![]() ��
��
��3�����������������ε�Ƶ�ʿ���������Ӧ�������εĸ��ʣ��ִ�ȫУ�������п�����ѧ�ɼ��������ȡ5����������ǡ��2���ɼ���![]() �ڵĸ���.
�ڵĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��������![]() ���ⳤΪ1���߶�
���ⳤΪ1���߶�![]() ������������
������������![]() ��
��![]() ����
����![]() ���������������____________��
���������������____________��
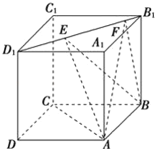
��![]() ��
��
��![]() ƽ��
ƽ��![]() ��
��
������![]() �����Ϊ��ֵ��
�����Ϊ��ֵ��
������ֱ��![]() ��
��![]() ���ɵĽ�Ϊ��ֵ��
���ɵĽ�Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������ij��������10����ÿ�²�Ʒ���ܳɱ�![]() ����Ԫ������²���
����Ԫ������²���![]() �������֮��������һ�����ݣ�
�������֮��������һ�����ݣ�
| 1.08 | 1.12 | 1.19 | 1.28 | 1.36 | 1.48 | 1.59 | 1.68 | 1.80 | 1.87 |
| 2.25 | 2.37 | 2.40 | 2.55 | 2.64 | 2.75 | 2.92 | 3.03 | 3.14 | 3.26 |
��1��ͨ����ɢ��ͼ�����ֿ������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ���������ϵ��
�Ĺ�ϵ���������ϵ��![]() ����˵����
����˵����
��2���ٽ������ܳɱ�![]() ���²���
���²���![]() ֮��Ļع鷽�̣���ͨ��������
֮��Ļع鷽�̣���ͨ��������![]() ����
����![]() �Ļع鷽�̣�����ij�²���Ϊ1.98���ʱ����Ʒ���ܳɱ�Ϊ������Ԫ��������ȷ��0.001��
�Ļع鷽�̣�����ij�²���Ϊ1.98���ʱ����Ʒ���ܳɱ�Ϊ������Ԫ��������ȷ��0.001��
��ע���ٲο����ݣ�![]() ��
��![]() ��
��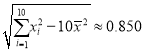 ��
��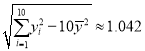 ��
��![]() .
.
�ڲο���ʽ�����ϵ��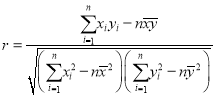 ��
��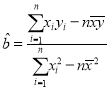 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪˫����![]() �����ҽ���ֱ�Ϊ
�����ҽ���ֱ�Ϊ![]() ��Բ
��Բ![]() ��˫�����ڵ�һ�����ڵĽ���ΪM����
��˫�����ڵ�һ�����ڵĽ���ΪM����![]() �����˫���ߵ�������Ϊ
�����˫���ߵ�������Ϊ
A. 2B. 3C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]()
![]() ��������Ϊ
��������Ϊ![]() ������ԭ��OΪԲ�ģ���ԲC�ij����᳤Ϊ�뾶��Բ��ֱ��
������ԭ��OΪԲ�ģ���ԲC�ij����᳤Ϊ�뾶��Բ��ֱ��![]() ���У�
����
��1������Բ�ı����̣�
��2����֪��ֱ��l���ҽ���F��������ԲC����A��B���㣬��֪Q������Ϊ![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ����������ֱ�Ϊ
����������ֱ�Ϊ![]() �����᳤Ϊ
�����᳤Ϊ![]() ��
��
����������Բ![]() �ı����̼������ʣ�
�ı����̼������ʣ�
����������![]() ��ֱ��
��ֱ��![]() ����Բ
����Բ![]() ����
����![]() ��
��![]() ���㣬����
���㣬����![]() ����
����![]() ����֤���ɵ�
����֤���ɵ�![]() ���ɵ�����
���ɵ�����![]() ����ֱ��
����ֱ��![]() �Գƣ�
�Գƣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������˶����ѳ�Ϊ�������ŵ��˶���ʽ��С������������Ҳ�д������Ѳ����������˶����������ѡȡ�����е�40�ˣ��С�Ů��20�ˣ�����¼������ijһ�����·���������������������£�
�Ա� ���� | 0��2000 | 2001��5000 | 5001��8000 | 8001��10000 | ��10000 |
�� | 1 | 2 | 3 | 6 | 8 |
Ů | 0 | 2 | 10 | 6 | 2 |
��1����֪ij��һ�����·��������8000����ϵͳ����Ϊ����������������Ϊ��и������������������������2��2�����������ݴ��ж��ܷ���95%���ϵİ�����Ϊ�����������������Ա����йأ�
������ | и���� | �ܼ� | |
�� | |||
Ů | |||
�ܼ� |
��2����С������40λ���Ѹ�����·������Ƶ�ʷֲ��������������ź���ÿ����·�����ĸ��ʷֲ����ִ�С���������ź�������ѡ2�ˣ�����ÿ����·������5000������X�ˣ�����10000������Y�ˣ�������|X��Y|����E�ķֲ��м���ѧ������
����K2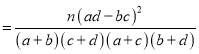 ��n��a+b+c+d��
��n��a+b+c+d��
P��K2��k0�� | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�����
�У�����![]() Ϊ���Σ�
Ϊ���Σ�![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() .
.
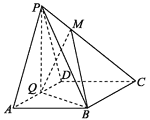
��1����֤��![]() ƽ��
ƽ��![]() ��
��
��2����![]() ���߶�
���߶�![]() �ϣ�
�ϣ�![]() ����ȷ��
����ȷ��![]() ��ֵ��ʹ
��ֵ��ʹ![]() ƽ��
ƽ��![]() ��
��
��3����![]() ƽ��
ƽ��![]() ��ƽ��
��ƽ��![]() ƽ��
ƽ��![]() ��������
��������![]() �Ĵ�С.
�Ĵ�С.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com