
分析 先求出函数的定义域,然后对函数f(x)进行求导,根据导函数大于0时原函数单调递增、导函数小于0时原函数单调递减对a分3种情况进行讨论
解答 解:f(x)的定义域为(0,+∞),
f′(x)=$\frac{a-1}{x}$+2ax=$\frac{2{ax}^{2}+a-1}{x}$,
①当a-1≥0时,f′(x)>0,故f(x)在(0,+∞)单调增加;
②当a≤0时,f′(x)<0,故f(x)在(0,+∞)单调减少;
③当0<a<1时,令f′(x)=0,解得x=$\sqrt{\frac{1-a}{2a}}$,
当x∈(0,$\sqrt{\frac{1-a}{2a}}$)时,f′(x)>0;
x∈( $\sqrt{\frac{1-a}{2a}}$,+∞)时,f′(x)<0,
故f(x)在(0,$\sqrt{\frac{1-a}{2a}}$)上单调增加,在( $\sqrt{\frac{1-a}{2a}}$,+∞)单调减.
点评 本题主要考查函数的单调性与其导函数正负之间的关系,考查分类讨论思想,是一道中档题.


科目:高中数学 来源:2016-2017学年江西吉安一中高二上段考一数学(理)试卷(解析版) 题型:填空题
如图,正方体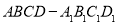 的棱长为1,点
的棱长为1,点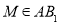 ,
,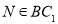 ,且
,且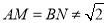 ,有以下四个结论:
,有以下四个结论:
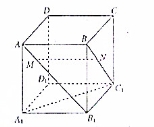
①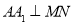 ;②
;② ;③
;③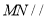 平面
平面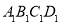 ;④
;④ 与
与 是异面直线.其中正确命题的序号是_______.(注:把你认为正确命题的序号都填上)
是异面直线.其中正确命题的序号是_______.(注:把你认为正确命题的序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
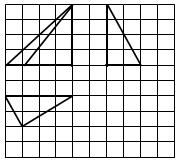 如图:网格上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面面积中的最大值为( )
如图:网格上的小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各面面积中的最大值为( )| A. | 16 | B. | 8 | C. | 2$\sqrt{13}$ | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
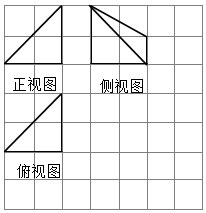 某几何体的三视图如图所示,图中小方格的长度为1,则该几何体的体积为( )
某几何体的三视图如图所示,图中小方格的长度为1,则该几何体的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | 2 | D. | $\frac{16}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
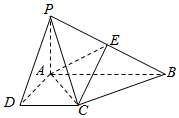 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,DC∥AB,PA=1,AB=2,PD=BC=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 三角形的内角是第一象限角或第二象限角 | |
| B. | 第一象限的角是锐角 | |
| C. | 第二象限的角比第一象限的角大 | |
| D. | 角α是第四象限角的充要条件是2kπ-$\frac{π}{2}$<α<2kπ(k∈Z) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com