【题目】某种水果的单个质量在500g以上视为特等品.随机抽取1000个该水果，结果有50个特等品.将这50个水果的质量数据分组，得到下边的频率分布表.
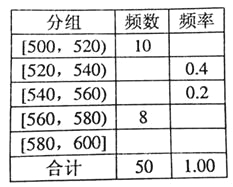
（1）估计该水果的质量不少于560g的概率；
（2）若在某批水果的检测中，发现有15个特等品，据此估计该批水果中没有达到特等品的个数.
【答案】（1）0.2；（2）285.
【解析】试题分析：本题主要考查频率分布表、频率的计算、分层抽样等基础知识，考查学生的分析问题解决问题的能力、计算能力.第一问，在
之间，利用“频率=频数÷样本总数”计算
范围内的频率0.2，在
范围内的频数为20，在
范围内的频数为10，在
范围内的频率为0.16，在
内的频率为0.04，频数为2，则第一问不少于560g的概率为
和
的频率之和；第二问，用分层抽样的方法列出表达式，解出未知数.
试题解析：（1）由已知可得该水果的质量不少于560g的概率
p＝0.16＋0.04＝0.2． 6分
（2）设该批水果中没有达到特等品的个数为x，则有
，解得x＝285． 12分
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：
【题目】已知f（x）=max{x2﹣ax+a，ax﹣a+1}，其中max{x，y}= 
． （Ⅰ）若对任意x∈R，恒有f（x）=x2﹣ax+a，求实数a的值；
（Ⅱ）若a＞1，求f（x）的最小值m（a）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】定义在R上的函数f（x），f（0）≠0，f（1）=2，当x＞0，f（x）＞1，且对任意a，b∈R，有f（a+b）=f（a）f（b）．
（1）求证：对任意x∈R，都有f（x）＞0；
（2）判断f（x）在R上的单调性，并用定义证明；
（3）求不等式f（3﹣2x）＞4的解集．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】从某小学随机抽取100名同学，将他们的身高（单位：厘米）数据绘制成频率分布直方图（如图）．若要从身高在[ 120 , 130），[130 ，140) , [140 , 150]三组内的学生中，用分层抽样的方法选取18人参加一项活动，则从身高在[140 ，150]内的学生中选取的人数应为 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】随着生活水平的提高，人们对空气质量的要求越来越高，某机构为了解公众对“车辆限行”的态度，随机抽查了50人，并将调查情况进行整理后制成下表：
（1）规定：年龄在
内的为青年人，年龄在
内的为中年人，根据以上统计数据填写下面
列联表：
（2）能否在犯错误的概率不超过0.025的前提下，认为赞成“车辆限行”与年龄有关？
参考公式和数据： 
，其中
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
