
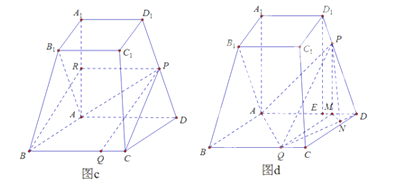
【题目】如图,已知四棱台![]() 上、下底面分别是边长为3和6的正方形,
上、下底面分别是边长为3和6的正方形,![]() ,且
,且![]() 底面
底面![]() ,点
,点![]() ,
,![]() 分别在棱
分别在棱![]() ,
,![]() 上.
上.
(1)若是![]() 是
是![]() 的中点,证明:
的中点,证明:![]() ;
;
(2若![]() //平面
//平面![]() ,二面角
,二面角![]() 的余弦值为
的余弦值为![]() ,求四面体
,求四面体![]() 的体积
的体积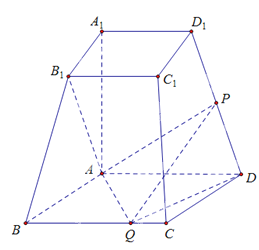
【答案】由题意得, A A 1 , A B , A D 两两垂直,以 A 为坐标原点, A B , A D , A A 1 所在直线分别为 x 轴 y 轴 z 轴,建立如图下图所示的空间直角坐标系,则相关各点的坐标为 A ( 0 , 0 , 0 ) , B 1 ( 3 , 0 , 6 ) , D ( 0 , 6 , 0 ) , D 1 ( 0 , 3 , 6 ) , Q ( 6 , m , 0 ) , 其中 m = B Q , 0 ≤ m ≤ 6 .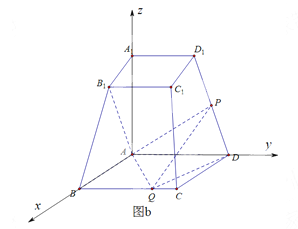
(1)若![]() 是
是![]() 的中点,则
的中点,则![]() 于是
于是![]() 所以
所以![]() .即
.即![]()
(2)由题意设知,![]() 是平面
是平面![]() 内的两个不共线向量.设
内的两个不共线向量.设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则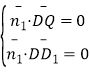 即
即![]() ,取
,取![]() 得
得![]() ,又平面
,又平面![]() 的一个法向量
的一个法向量![]() 所以
所以![]()
![]() 而二面角P-QD-A的余弦值为
而二面角P-QD-A的余弦值为![]() , 因此
, 因此![]() =
=![]() 解得.m=4或者m=8(舍去)此时Q(6,4,0)设
解得.m=4或者m=8(舍去)此时Q(6,4,0)设![]() 而
而![]() =(0,-3,6)由此得点P
=(0,-3,6)由此得点P![]()
![]() 因为PQ//平面ABB1A1且平面ABB1A1的一个法向量
因为PQ//平面ABB1A1且平面ABB1A1的一个法向量![]() =(0,1,0)所以,
=(0,1,0)所以,![]() ·
·![]() =0即,
=0即,![]() 亦即得
亦即得![]() 从而P(0,4,4,)于是将四面体ADPQ视为以
从而P(0,4,4,)于是将四面体ADPQ视为以![]() ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积
ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积![]()
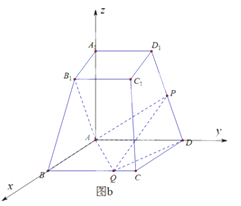


【解析】由题意得,![]() 两两垂直,以
两两垂直,以![]() 为坐标原点,
为坐标原点,![]() 所在直线分别为
所在直线分别为![]() 轴
轴![]() 轴
轴![]() 轴,建立如图下图所示的空间直角坐标系,则相关各点的坐标为
轴,建立如图下图所示的空间直角坐标系,则相关各点的坐标为![]() 其中
其中![]() .
.
(1)若![]() 是
是![]() 的中点,则
的中点,则![]() 于是
于是![]() 所以
所以![]() .即
.即![]()
(2)由题意设知,![]() 是平面
是平面![]() 内的两个不共线向量.设
内的两个不共线向量.设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则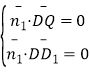 即
即![]() ,取
,取![]() 得
得![]() ,又平面
,又平面![]() 的一个法向量
的一个法向量![]() 所以
所以![]()
![]() 而二面角P-QD-A的余弦值为
而二面角P-QD-A的余弦值为![]() ,因此
,因此![]() =
=![]() 解得.m=4或者m=8(舍去)此时Q(6,4,0)设
解得.m=4或者m=8(舍去)此时Q(6,4,0)设![]() 而
而![]() =(0,-3,6)由此得点P
=(0,-3,6)由此得点P![]()
![]() 因为PQ//平面ABB1A1且平面ABB1A1的一个法向量
因为PQ//平面ABB1A1且平面ABB1A1的一个法向量![]() =(0,1,0)所以,
=(0,1,0)所以,![]() ·
·![]() =0即,
=0即,![]() 亦即得
亦即得![]() 从而P(0,4,4,)于是将四面体ADPQ视为以
从而P(0,4,4,)于是将四面体ADPQ视为以![]() ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积
ADQ为底面的三棱锥P-ADQ 则其高h=4故四面体ADPQ的体积![]()




【考点精析】通过灵活运用向量的三角形法则和平面向量的坐标运算,掌握三角形加法法则的特点:首尾相连;三角形减法法则的特点:共起点,连终点,方向指向被减向量;坐标运算:设![]() ,
,![]() 则
则![]() ;
;![]() ;设
;设![]() ,则
,则![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】![]() 全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.求:(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播2015年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前20名的“省级卫视新闻台”的融合指数进行分组统计,结果如表所示.求:(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
组号 | 分组 | 频数 |
1 | [4,5) | 2 |
2 | [5,6) | 8 |
3 | [6,7) | 7 |
4 | [7,8] | 3 |
(1)现从融合指数在[4,5)和[7,8]内的“省级卫视新闻台”中随机抽取2家进行调研,求至少有1家的融合指数在[7,8]的概率;
(2)根据分组统计表求这20家“省级卫视新闻台”的融合指数的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 已知2件次品和3件正品放在一起,现需要通过检测将其区分,每次随机检测一件产品,检测后不放回,直到检测出2件次品或者检测出3件正品时检测结束.
(1)求第一次检测出的是次品且第二次检测出的是正品的概率;
(2)已知每检测一件产品需要费用100元,设X表示直到检测出2件次品或者检测出3件正品时所 需要的检测费用(单位:元),求X的分布列和均值(数学期望).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】汽车的“燃油效率”是指汽车每消耗1升汽油行驶的里程,下图描述了甲、乙、丙三辆汽车在不同速度下的燃油效率情况. 下列叙述中正确的是( )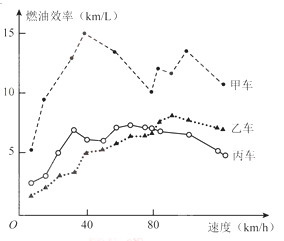
A.消耗1升汽油,乙车最多可行驶5千米
B.以相同速度行驶相同路程,三辆车中,甲车消耗汽油最多
C.甲车以80千米/小时的速度行驶1小时,消耗10升汽油
D.某城市机动车最高限速80千米/小时.相同条件下,在该市用丙车比用乙车更省油
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=![]() )
)
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) 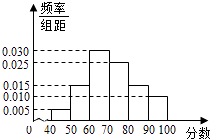
A.588
B.480
C.450
D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C: ![]() +
+ ![]() =1,直线l:
=1,直线l: ![]() (t为参数)
(t为参数)
(1)写出曲线C的参数方程,直线l的普通方程.
(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在(0,+∞)的函数f(x),其导函数为f′(x),满足:f(x)>0且 ![]() 总成立,则下列不等式成立的是( )
总成立,则下列不等式成立的是( )
A.e2e+3f(e)<e2ππ3f(π)
B.e2e+3f(π)>e2ππ3f(e)
C.e2e+3f(π)<e2ππ3f(e)
D.e2e+3f(e)>e2ππ3f(π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com