
【题目】生产甲乙两种精密电子产品,用以下两种方案分别生产出甲乙产品共![]() 种,现对这两种方案生产的产品分别随机调查了各
种,现对这两种方案生产的产品分别随机调查了各![]() 次,得到如下统计表:
次,得到如下统计表:
①生产![]() 件甲产品和
件甲产品和![]() 件乙产品
件乙产品
正次品 | 甲正品 甲正品 乙正品 | 甲正品 甲正品 乙次品 | 甲正品 甲次品 乙正品 | 甲正品 甲次品 乙次品 | 甲次品 甲次品 乙正品 | 甲次品 甲次品 乙次品 |
频 数 |
|
|
|
|
|
|
②生产![]() 件甲产品和
件甲产品和![]() 件乙产品
件乙产品
正次品 | 乙正品 乙正品 甲正品 | 乙正品 乙正品 甲次品 | 乙正品 乙次品 甲正品 | 乙正品 乙次品 甲次品 | 乙次品 乙次品 甲正品 | 乙次品 乙次品 甲次品 |
频 数 |
|
|
|
|
|
|
已知生产电子产品甲![]() 件,若为正品可盈利
件,若为正品可盈利![]() 元,若为次品则亏损
元,若为次品则亏损![]() 元;生产电子产品乙
元;生产电子产品乙![]() 件,若为正品可盈利
件,若为正品可盈利![]() 元,若为次品则亏损
元,若为次品则亏损![]() 元.
元.
(I)按方案①生产![]() 件甲产品和
件甲产品和![]() 件乙产品,求这
件乙产品,求这![]() 件产品平均利润的估计值;
件产品平均利润的估计值;
(II)从方案①②中选其一,生产甲乙产品共![]() 件,欲使
件,欲使![]() 件产品所得总利润大于
件产品所得总利润大于![]() 元的机会多,应选用哪个?
元的机会多,应选用哪个?
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C: ![]() 经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
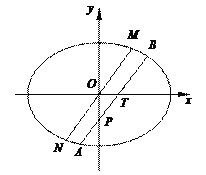
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求 ![]() 的值;
的值;
(3)记直线l与y轴的交点为P.若![]() ,求直线l的斜率k.
,求直线l的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数z=k﹣2i(k∈R)的共轭复数 ![]() ,且z﹣(
,且z﹣( ![]() ﹣i)=
﹣i)= ![]() ﹣2i.
﹣2i.
(1)求k的值;
(2)若过点(0,﹣2)的直线l的斜率为k,求直线l与曲线y= ![]() 以及y轴所围成的图形的面积.
以及y轴所围成的图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列各式中,所得数值最小的是( )
A.sin50°cos39°﹣sin40°cos51°
B.﹣2sin240°+1
C.2sin6°cos6°
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}满足a3=7,a5+a7=26,数列{an}的前n项和Sn .
(1)求an及Sn;
(2)令bn= ![]() (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】长方体ABCD﹣A1B1C1D1中AB=AA1=2,AD=1,E为CC1的中点,则异面直线BC1与AE所成角的余弦值为( )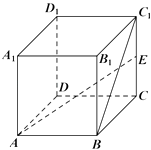
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com