
分析 由已知向量模的等式两边平方得到两个向量的模的关系,以及向量的夹角公式计算即可.
解答 解:∵|$\overrightarrow{a}$|=2,|2$\overrightarrow{a}$-$\overrightarrow{b}$|=2$\sqrt{7}$,
∴|2$\overrightarrow{a}$-$\overrightarrow{b}$|2=(2$\sqrt{7}$)2,
∴4|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2-4$\overrightarrow{a}$•$\overrightarrow{b}$=28,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=-3+$\frac{1}{4}$|$\overrightarrow{b}$|2,
∵向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为60°,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos60°=|$\overrightarrow{b}$|,
∴-3+$\frac{1}{4}$|$\overrightarrow{b}$|2=|$\overrightarrow{b}$|,
解得|$\overrightarrow{b}$|=6,
故答案为:6.
点评 本题考查了向量的数量积、模的平方与向量的平方相等的运用,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
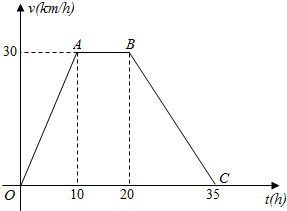 据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).
据气象中心观察和预测:发生于 地的沙尘暴一直向正南方向移动,其移动速度v(km/h)与时间t的函数图象如图所示,过线段OC 上一点T(t,0)作横轴的垂线l,梯形OABC在直线l 左侧部分的面积即为t(h)内沙尘暴所经过的路程s(km).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
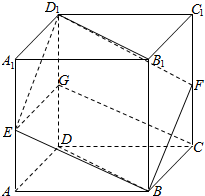 如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.
如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com