某地区的农产品A第z天(1≤x≤20)的销售价格p=40-|x一6|(元/千克),一农户在第x天(1≤x≤20)农产品A的销售量q=30+|x一8|(千克).
(1)求该农户在第7天销售农产品的收入;
(2)问这20天中该农户在哪一天的销售收入最大?最大收入为多少?
解:(1)由已知第7天的销售价格p=40-|x-6|=40-|7-6|=39,销售量q=30+|x-8|=30+|7-8|=31.
∴第7天的销售收入W
7=pq=39×31=1209(元).
(2)设第x天的销售收入为W
x,则W
x=
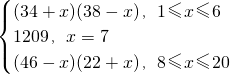
当1≤x≤6时,Wx=(34+x)(38-x)≤[
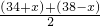
]
2=1296(当且仅当x=2时取等号),∴当x=2时有最大值W
2=1296;
当8≤x≤20时,W
x=(46-x)(22+x)≤[
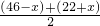
]
2=1156(当且仅当x=12时取等号),∴当x=12时有最大值W
12=1936;
由于W
2>W
7>W
12,所以,第2天该农户的销售收入最大.
分析:(1)第7天的销售价格p=40-|x-6|=40-|7-6|=39,销售量q=30+|x-8|=30+|7-8|=31,从而可得第7天的销售收入;
(2)若设第x天的销售收入为W
x,则Wx=pq=(40-|x-6|)(30+|x-8|),去掉绝对值后是分段函数,求得函数W
x的每一段的最大值,并通过比较得出,第几天该农户的销售收入最大.
点评:本题考查了含有绝对值的函数模型的应用;含有绝对值的函数,通常转化为分段函数来解答,本题是中档题目.

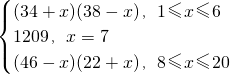
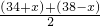 ]2=1296(当且仅当x=2时取等号),∴当x=2时有最大值W2=1296;
]2=1296(当且仅当x=2时取等号),∴当x=2时有最大值W2=1296;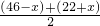 ]2=1156(当且仅当x=12时取等号),∴当x=12时有最大值W12=1936;
]2=1156(当且仅当x=12时取等号),∴当x=12时有最大值W12=1936;
