
����Ŀ����x�ᡢy���������ϵĵ�λ�����ֱ��� ![]() ��
�� ![]() ������ƽ���ϵ���An��Bn��n��N*���ֱ���������������������
������ƽ���ϵ���An��Bn��n��N*���ֱ��������������������� ![]() =
= ![]() ��
�� ![]() =
= ![]() +
+ ![]() ����
���� ![]() =4
=4 ![]() ��
�� ![]() =
= ![]() ��4
��4 ![]() ��
��
��1��� ![]() ��
�� ![]() �����꣬�����
�����꣬����� ![]() �����ꣻ
�����ꣻ
��2������OAnBn+1�������an �� ��an��n��N*���ı���ʽ��
��3�����ڣ�2���е�an �� �Ƿ����������Ȼ��M����һ��n��N*����an��M�����������ڣ����M���������ڣ�˵�����ɣ�
���𰸡�
��1���⣺ ![]() =
= ![]() +
+ ![]() =
= ![]() +
+ ![]() +
+ ![]() =
= ![]() +2
+2 ![]() =��1��2����
=��1��2���� ![]() =2
=2 ![]() +3
+3 ![]() =��2��3��
=��2��3��
![]() =��n��1��
=��n��1�� ![]() +n
+n ![]() =��n��1��n��
=��n��1��n��
��2���⣺An��n��1��n����������ֱ�߷���y=x+1����˵�An��ֱ��y=x+1�ϣ�
![]() =��1+1��
=��1+1�� ![]() +��+
+��+ ![]() ��
�� ![]() ����4
����4 ![]() =
= ![]() ��
�� ![]() ��
��
���OAnBn+1�����an= ![]() =
= ![]()
��3���⣺��t=n+1����t��2��t��N+����an=4t+ ![]() ��6��
��6��
y=4t+ ![]() ����y��=4��
����y��=4�� ![]() ��0��[2��+�ޣ��Ϻ������
��0��[2��+�ޣ��Ϻ������
��an=4t+ ![]() ��6��3��
��6��3��
�߶�һ��n��N*����an��M������
��M��3��
��M�����ֵΪ3
����������1�����������ļӷ�����д�� ![]() ��
�� ![]() �����꣬�����
�����꣬����� ![]() �����ꣻ��2��An��n��1��n����������ֱ�߷���y=x+1����˵�An��ֱ��y=x+1�ϣ�
�����ꣻ��2��An��n��1��n����������ֱ�߷���y=x+1����˵�An��ֱ��y=x+1�ϣ� ![]() =��1+1��
=��1+1�� ![]() +��+
+��+ ![]() ��
�� ![]() ����4
����4 ![]() =
= ![]() ��
�� ![]() ��������an��n��N*���ı���ʽ����3����t=n+1����t��2��t��N+����an=4t+
��������an��n��N*���ı���ʽ����3����t=n+1����t��2��t��N+����an=4t+ ![]() ��6��an=4t+
��6��an=4t+ ![]() ��6��3�����ɵó����ۣ�
��6��3�����ɵó����ۣ�


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017��������ɽ��ģ����֪��Բ������![]() ������
������![]() ���Ͻصõ��ҳ�Ϊ4���Ƕ�ԲԲ�ĵĹ켣Ϊ����C��
���Ͻصõ��ҳ�Ϊ4���Ƕ�ԲԲ�ĵĹ켣Ϊ����C��
������ֱ��![]() ������CΧ�ɵ����������
������CΧ�ɵ����������
����![]() ��ֱ��
��ֱ��![]() �ϣ���
�ϣ���![]() ������
������![]() ������C������
������C������![]() ��
��![]() ���е�ֱ�Ϊ
���е�ֱ�Ϊ![]() ��
��![]() ��֤�������ڳ���
��֤�������ڳ���![]() ��ʹ��
��ʹ��![]() ������
������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������{an}��ǰn���ΪSn �� �����������������n����Sn=2an��3n��
��1����bn=an+3����֤������{bn}�ǵȱ����У������{an}��ͨ�ʽ��
��2��������{nan}��ǰn��ͣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ij�β����У���6λͬѧ��ƽ���ɼ�Ϊ75�֣���xn��ʾ���Ϊn��n=1��2������6����ͬѧ���óɼ�����ǰ5λͬѧ�ijɼ����£�
���n | 1 | 2 | 3 | 4 | 5 |
�ɼ�xn | 70 | 76 | 72 | 70 | 72 |
��1�����6λͬѧ�ijɼ�x6 �� ����6λͬѧ�ɼ��ı���s��
��2����ǰ5λͬѧ�У������ѡ2λͬѧ����ǡ��1λͬѧ�ɼ������䣨68��75���еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]() =��1��2����
=��1��2���� ![]() =��x��1����
=��x��1����
��1������ ![]() +2
+2 ![]() ���ͣ�2
���ͣ�2 ![]() ��
�� ![]() ��ʱ����x��ֵ��
��ʱ����x��ֵ��
��2�������� ![]() ������
������ ![]() �ļн�Ϊ��ǣ���x��ȡֵ��Χ��
�ļн�Ϊ��ǣ���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017����һģ20����֪����![]() �����к���
�������![]() ��
��![]() ��
��
��1������![]() ��
��![]() �������߷�����
�������߷�����
��2����![]() ʱ������
ʱ������![]() ��
��![]() �ϵ����ֵ��
�ϵ����ֵ��
��3����![]() ʱ�����ڸ�����������
ʱ�����ڸ�����������![]() ���ʺ���
���ʺ���![]() �Ƿ�����㣿��˵�����ɣ����ο�����
�Ƿ�����㣿��˵�����ɣ����ο�����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2017�Ͼ�һģ19���躯��![]() ��
��![]() ��
��
��1����![]() ʱ�������
ʱ�������![]() �ķ���
�ķ���![]() ������
������![]() Ϊ��Ȼ�����ĵ�������
Ϊ��Ȼ�����ĵ�������
��2������![]() �ĵ��������䣻
�ĵ��������䣻
��3����![]() ʱ���Ǻ���
ʱ���Ǻ���![]() ���Ƿ��������
���Ƿ��������![]() ��ʹ�ù���
��ʹ�ù���![]() �IJ���ʽ
�IJ���ʽ
![]() �н⣿�����ڣ������
�н⣿�����ڣ������![]() ����Сֵ���������ڣ���˵��������
����Сֵ���������ڣ���˵��������
���ο����ݣ�![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ��������״����ijУ�����ȡ��һ��ѧ���������أ���ͳ�ƣ�����ѧ�����������ݣ���λ��ǧ�ˣ�ȫ������45��70֮�䣮�����ݷֳ�����5�飺��1��[45��50������2��[50��55������3��[55��60������4��[60��65������5��[65��70]���õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ���ֲ��÷ֲ�����ķ������ӵ�3��4��5���������ȡ6��ѧ�������죮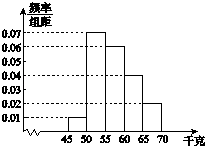
��1����ÿ���ȡ��ѧ��������
��2������6��ѧ�����ٴ������ȡ2��ѧ�����и��죬����2��ѧ������ͬһ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Ϊ100��������Ƶ�ʷֲ�ֱ��ͼ��������������[6,10)�ڵ�Ƶ�ʺ�Ƶ���ֱ��ǣ� ��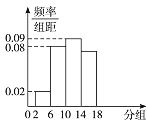
A.0.32,32 ����
B.0.08,8 ��
C.0.24,24 ����
D.0.36,36
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com