
 ,乙解出它的概率为
,乙解出它的概率为 ,丙解出它的概率为
,丙解出它的概率为 ,则
,则
|
 B.
B. C.
C.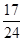 D.1
D.1科目:高中数学 来源:不详 题型:单选题
A.
| B.
| C.
| D.
|
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
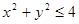 确定的平面区域为
确定的平面区域为 ,
,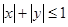 确定的平面区域为
确定的平面区域为
 内任取
内任取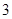 个整点,求这些整点中恰有
个整点,求这些整点中恰有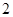 个整点在区域
个整点在区域 内的概率;
内的概率; 内任取
内任取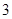 个点,记这
个点,记这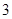 个点在区域
个点在区域 内的个数为
内的个数为 ,求
,求 的分布列,数学期望
的分布列,数学期望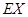 及方差
及方差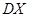 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
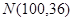 ,那么考试成绩在区间(88,112)内的概率是( )
,那么考试成绩在区间(88,112)内的概率是( )| A.0.683 | B.0.371 | C.0.954 | D.0.997 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
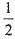 ,通晓中文和日语的概率为
,通晓中文和日语的概率为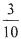 .若通晓中文和韩语的人数不超过3人.
.若通晓中文和韩语的人数不超过3人.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 正常工作的概率分别为
正常工作的概率分别为 ,将它们中某两个元件并联后再和第三个元件串联接入电路,在如图的电路中,电路不发生故障的概率是 ( )
,将它们中某两个元件并联后再和第三个元件串联接入电路,在如图的电路中,电路不发生故障的概率是 ( )
A.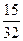 | B. | C.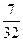 | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com