
已知函数f(x)=ax3-3ax,g(x)=bx2+clnx,且g(x)在点(1,g(1))处的切线方程为2y-1=0.
(1)求g(x)的解析式;
(2)设函数G(x)=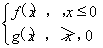 若方程G(x)=a2有且仅有四个解,求实数a的取值范围.
若方程G(x)=a2有且仅有四个解,求实数a的取值范围.
(1)g(x)=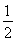 x2-lnx(2)
x2-lnx(2)
【解析】(1)g′(x)=2bx+ 由条件,得
由条件,得 即
即 ∴b=
∴b=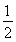 ,c=-1,
,c=-1,
∴g(x)=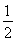 x2-lnx.
x2-lnx.
(2)G(x)=
当x>0时,G(x)=g(x)=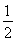 x2-lnx,g′(x)=x-
x2-lnx,g′(x)=x-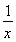 =
=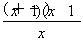 .
.
令g′(x)=0,得x=1,且当x∈(0,1),g′(x)<0,x∈(1,+∞),g′(x)>0,
∴g(x)在(0,+∞)上有极小值,即最小值为g(1)=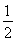 .
.
当x≤0时,G(x)=f(x)=ax3-3ax,f′(x)=3ax2-3a=3a(x+1)(x-1).
令f′(x)=0,得x=-1.①若a=0,方程G(x)=a2不可能有四个解;
②若a<0时,当x∈(-∞,-1),f′(x)<0,当x∈(-1,0),f′(x)>0,∴f(x)在(-∞,0]上有极小值,即最小值为f(-1)=2a.又f(0)=0,∴G(x)的图象如图①所示,从图象可以看出方程G(x)=a2不可能有四个解;
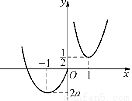 ,①)
,①) 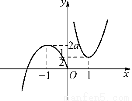 ,②)
,②)
③若a>0时,当x∈(-∞,-1),f′(x)>0,当x∈(-1,0),f′(x)<0,∴f(x)在(-∞,0]上有极大值,即最大值为f(-1)=2a.又f(0)=0,∴G(x)的图象如图②所示.从图象可以看出方程G(x)=a2若有四个解,必须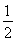 <a2<2a,∴
<a2<2a,∴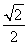 <a<2.综上所述,满足条件的实数a的取值范围是
<a<2.综上所述,满足条件的实数a的取值范围是


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第9课时练习卷(解析版) 题型:填空题
若函数f(x)=log2|ax-1|(a>0),当x≠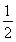 时,有f(x)=f(1-x),则a=________.
时,有f(x)=f(1-x),则a=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第7课时练习卷(解析版) 题型:填空题
已知函数f(x)= 则f(2+log23)=________.
则f(2+log23)=________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第6课时练习卷(解析版) 题型:填空题
已知函数f(x)=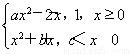 是偶函数,直线y=t与函数y=f(x)的图象自左向右依次交于四个不同点A、B、C、D.若AB=BC,则实数t的值为________.
是偶函数,直线y=t与函数y=f(x)的图象自左向右依次交于四个不同点A、B、C、D.若AB=BC,则实数t的值为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第6课时练习卷(解析版) 题型:解答题
已知二次函数f(x)=ax2+bx+c图象的顶点为(-1,10),且方程ax2+bx+c=0的两根的平方和为12,求二次函数f(x)的表达式.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第5课时练习卷(解析版) 题型:填空题
已知直线y=a与函数f(x)=2x及g(x)=3·2x的图象分别相交于A、B两点,则A、B两点之间的距离为________.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第5课时练习卷(解析版) 题型:解答题
已知函数y=f(x)的图象如图所示,请根据已知图象作出下列函数的图象:
①y=f(x+1);②y=f(x)+2;
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第4课时练习卷(解析版) 题型:解答题
设函数f(x)是定义在(-1,1)上的偶函数,在(0,1)上是增函数,若f(a-2)-f(4-a2)<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年高考数学总复习考点引领+技巧点拨第二章第2课时练习卷(解析版) 题型:填空题
已知函数f(x)=x2-2x,x∈[a,b]的值域为[-1,3],则b-a的取值范围是________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com