
分析 法1:x=0时,可以求出y=1,而x≠0时,可将原函数变成$y=1-\frac{1}{x+\frac{1}{x}+1}$,这样可看出需讨论x>0和x<0,对于每种情况可根据基本不等式求出$x+\frac{1}{x}$的范围,进而求出$\frac{1}{x+\frac{1}{x}+1}$的范围,从而得出y的范围,从而最后对求得的y值和y的范围求并集即可得出原函数的值域.
法2:由原函数得,yx2+yx+y=x2+1,利用判别式法可得答案.
解答 解:法1:①x=0时,y=1;
②x≠0时,$y=\frac{{x}^{2}+1}{{x}^{2}+x+1}=\frac{{x}^{2}+x+1-x}{{x}^{2}+x+1}=1-\frac{x}{{x}^{2}+x+1}$=$1-\frac{1}{x+\frac{1}{x}+1}$;
1)x>0时,$x+\frac{1}{x}≥2$,x=1时取“=”;
∴$0<\frac{1}{x+\frac{1}{x}+1}≤\frac{1}{3}$;
∴$\frac{2}{3}≤y<1$;
2)x<0时,$x+\frac{1}{x}=-[(-x)+\frac{1}{-x}]≤-2$,x=-1时取“=”;
∴$-1≤\frac{1}{x+\frac{1}{x}+1}<0$;
∴1<y≤2;
∴综上得原函数的值域为$[\frac{2}{3},2]$.
法2:由原函数得,yx2+yx+y=x2+1;
整理得,(y-1)x2+yx+y-1=0,看成关于x的方程,方程有解;
①若y=1,x=0,满足方程有解;
②若y≠1,则:△=y2-4(y-1)2≥0;
解得$\frac{2}{3}≤y≤2$;
∴综上得,原函数的值域为$[\frac{2}{3},2]$.
点评 考查函数值域的概念,分离常数法的运用,将原函数变成可以利用基本不等式求y的范围从而求值域的方法,注意应用基本不等式求y的范围所具备的条件.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
| A. | 0<a<$\frac{\sqrt{3}}{3}$ | B. | 0<a<$\frac{\sqrt{6}}{6}$ | C. | 1<a<$\sqrt{3}$ | D. | 1<a<$\sqrt{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | 13(lg2)2 | C. | 10 | D. | 10(lg2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
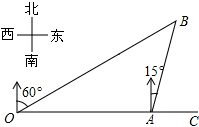
| A. | 4km | B. | 2$\sqrt{3}$km | C. | 2$\sqrt{2}$km | D. | ($\sqrt{3}$+1)km |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com