
分析 由双曲线有共同渐近线的特点设出双曲线的方程为$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=λ(λ≠0),代入点A($\sqrt{3}$,2$\sqrt{5}$),求出λ再化简即可.
解答 解:设方程为$\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{2}$=λ(λ≠0),
代入点A($\sqrt{3}$,2$\sqrt{5}$),可得$\frac{3}{3}-\frac{20}{2}$=λ,
∴λ=-9,
∴双曲线的方程为$\frac{{y}^{2}}{18}-\frac{{x}^{2}}{27}$=1.
故答案为:$\frac{{y}^{2}}{18}-\frac{{x}^{2}}{27}$=1.
点评 本题考查双曲线特有的性质:渐近线,熟练掌握双曲线有共同渐近线的方程特点是解题的关键.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
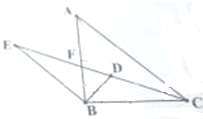 已知等腰直角三角形ABC中,∠ABC=90°,∠ABC和∠ACB的角平分线交于点D,延长CD交AC的平行线BE于点E.
已知等腰直角三角形ABC中,∠ABC=90°,∠ABC和∠ACB的角平分线交于点D,延长CD交AC的平行线BE于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{π}{4}$-$\frac{1}{2}$ | C. | $\frac{π}{4}$ | D. | 1-$\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
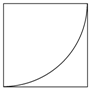 一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.
一块正方形薄铁片的边长为4cm,以它的一个顶点为圆心,一边长为半径画弧,沿弧剪下一个扇形(如图),用这块扇形铁片围成一个圆锥筒,则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
| 态度 年龄 | 赞成 | 不赞成 | 总计 |
| 中青年 | |||
| 中老年 | |||
| 总计 |
| X2 | ≤2.706 | >2.706 | >3.841 | >6.635 |
| A、B关联性 | 无关联 | 90% | 95% | 99% |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=g(x)在(0,$\frac{π}{2}$)上递减 | B. | y=g(x)在(0,$\frac{π}{6}$)上递减 | ||
| C. | y=g(x)在(0,$\frac{π}{2}$)上递增 | D. | y=g(x)在(0,$\frac{π}{6}$)上递增 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com