
【题目】已知![]() .
.
(1)若![]() ,求
,求![]() 在
在![]() 上的最小值;
上的最小值;
(2)求![]() 的极值点;
的极值点;
(3)若![]() 在
在![]() 内有两个零点,求
内有两个零点,求![]() 的取值范围.
的取值范围.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象在点
的图象在点![]() 处的切线为
处的切线为![]() ,若函数
,若函数![]() 满足
满足![]() (其中
(其中![]() 为函数
为函数![]() 的定义域,当
的定义域,当![]() 时,
时,![]() 恒成立,则称
恒成立,则称![]() 为函数
为函数![]() 的“转折点”,已知函数
的“转折点”,已知函数![]() 在区间
在区间![]() 上存在一个“转折点”,则
上存在一个“转折点”,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】又到了品尝小龙虾的季节,小龙虾近几年来被称作是“国民宵夜”风靡国内外.在巨大的需求市场下,湖北的小龙虾产量占据了全国的半壁江山,湖北某地区近几年的小龙虾产量统计如下表:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 |
年份代码 | 1 | 2 | 3 | 4 | 5 | 6 |
年产量 | 6.6 | 6.9 | 7.4 | 7.7 | 8 | 8.4 |
(1)根据表中数据,建立![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据线性回归方程预测2019年该地区农产品的年产量.
附:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: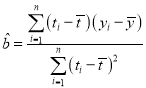 ,
,![]() .(参考数据:
.(参考数据:![]() ,计算结果保留小数点后两位).
,计算结果保留小数点后两位).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由于近几年我国多地区的雾霾天气,引起口罩热销,某厂家拟在2017年举行促销活动,经调查该批口罩销售量![]() 万件(生产量与销售量相等)与促销费用
万件(生产量与销售量相等)与促销费用![]() 万元满足
万元满足![]() (其中
(其中![]() ,
,![]() 为常数).已知生产该批口罩还要投入成本
为常数).已知生产该批口罩还要投入成本![]() 万元(不包含促销费用),口罩的销售价格定为
万元(不包含促销费用),口罩的销售价格定为![]() 元/件.
元/件.
(1)将该批口罩的利润![]() 万元表示为促销费用
万元表示为促销费用![]() 万元的函数;
万元的函数;
(2)当促销费用投入多少万元时,该厂家的利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线方程为y2=-4x,直线l的方程为2x+y-4=0,在抛物线上有一动点A,点A到y轴的距离为m,到直线l的距离为n,则m+n的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“新零售”模式的背景下,某大型零售公司推广线下分店,计划在S市的A区开设分店,为了确定在该区开设分店的个数,该公司对该市已开设分店的其他区的数据作了初步处理后得到下列表格.记x表示在各区开设分店的个数,y表示这个x个分店的年收入之和.

(1)该公司已经过初步判断,可用线性回归模型拟合y与x的关系,求y关于x的线性回归方程![]()
(2)假设该公司在A区获得的总年利润z(单位:百万元)与x,y之间的关系为![]() ,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
,请结合(1)中的线性回归方程,估算该公司应在A区开设多少个分店时,才能使A区平均每个分店的年利润最大?
(参考公式:![]() ,其中
,其中 ,
,![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高一(1)班参加校生物竞赛学生的成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题:

(1)求高一(1)班参加校生物竞赛的人数及分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间的矩形的高;
(2)若要从分数在[80,100]之间的学生中任选2人进行某项研究,求至少有1人分数在[90,100]之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() 为坐标原点)的斜率分别为
为坐标原点)的斜率分别为![]() ,
,![]() ,
,![]() ,
,![]() ,若
,若![]() .
.
(1)是否存在实数![]() ,满足
,满足![]() ,并说明理由;
,并说明理由;
(2)求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列判断正确的是( )
A.两圆锥曲线的离心率分别为![]() ,则“
,则“![]() ”是“两圆锥曲线均为椭圆”的充要条件.
”是“两圆锥曲线均为椭圆”的充要条件.
B.已知![]() 为圆
为圆![]() 内异于圆心的一点,则直线
内异于圆心的一点,则直线![]() 与该圆相交.
与该圆相交.
C.设![]() 是实数,若方程
是实数,若方程![]() 表示双曲线,则
表示双曲线,则![]() .
.
D.命题![]() 的否定是
的否定是![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com