
【题目】如图,四棱锥S﹣ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( ) 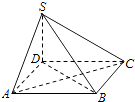
A.AC⊥SB
B.AB∥平面SCD
C.SA与平面SBD所成的角等于SC与平面SBD所成的角
D.AB与SC所成的角等于DC与SA所成的角
【答案】D
【解析】解:∵SD⊥底面ABCD,底面ABCD为正方形,
∴连接BD,则BD⊥AC,根据三垂线定理,可得AC⊥SB,故A正确;
∵AB∥CD,AB平面SCD,CD平面SCD,
∴AB∥平面SCD,故B正确;
∵SD⊥底面ABCD,
∠ASO是SA与平面SBD所成的角,∠CSO是SC与平面SBD所成的,
而△SAO≌△CSO,
∴∠ASO=∠CSO,即SA与平面SBD所成的角等于SC与平面SBD所成的角,故C正确;
∵AB∥CD,∴AB与SC所成的角是∠SCD,DC与SA所成的角是∠SAB,
而这两个角显然不相等,故D不正确;
故选D.
【考点精析】利用直线与平面垂直的性质对题目进行判断即可得到答案,需要熟知垂直于同一个平面的两条直线平行.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:
【题目】已知直线l与圆C:x2+y2+2x﹣4y+a=0相交于A,B两点,弦AB的中点为M(0,1).
(1)求实数a的取值范围以及直线l的方程;
(2)若圆C上存在动点N使CN=2MN成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a≠0,集合A={x|x2﹣x﹣6<0},B={x|x2+2x﹣8≥0},C={x|x2﹣4ax+3a2<0},且C(A∩RB).求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业为了对新研发的一批产品进行合理定价,将产品按事先拟定的价格进行试销,得到一组销售数据![]() ,如表所示:
,如表所示:

已知![]()
(1)求![]() 的值
的值
(2)已知变量![]() 具有线性相关性,求产品销量
具有线性相关性,求产品销量![]() 关于试销单价
关于试销单价![]() 的线性回归方程
的线性回归方程![]() 可供选择的数据
可供选择的数据![]()
(3)用![]() 表示(2)中所求的线性回归方程得到的与
表示(2)中所求的线性回归方程得到的与![]() 对应的产品销量的估计值。当销售数据
对应的产品销量的估计值。当销售数据![]() 对应的残差的绝对值
对应的残差的绝对值![]() 时,则将销售数据
时,则将销售数据![]() 称为一个“好数据”。试求这6组销售数据中的 “好数据”。
称为一个“好数据”。试求这6组销售数据中的 “好数据”。
参考数据:线性回归方程中![]() 的最小二乘估计分别是
的最小二乘估计分别是
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(a,0)(a>0),B(0,a),C(﹣4,0),D(0,4)设△AOB的外接圆圆心为E. 
(1)若⊙E与直线CD相切,求实数a的值;
(2)设点P在圆E上,使△PCD的面积等于12的点P有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P﹣ABC中,△ABC是等边三角形,D是AC的中点,PA=PC,二面角P﹣AC﹣B的大小为60°; 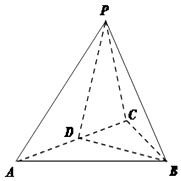
(1)求证:平面PBD⊥平面PAC;
(2)求AB与平面PAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() ,g(x)=xlnx﹣a(x﹣1).
,g(x)=xlnx﹣a(x﹣1).
(1)求函数f(x)在点(4,f(4))处的切线方程;
(2)若对任意x∈(0,+∞),不等式g(x)≥0恒成立,求实数a的取值的集合M;
(3)当a∈M时,讨论函数h(x)=f(x)﹣g(x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(1,3)B(3,1),C(﹣1,0)求:
(1)求BC及BC边上的中线所在直线的方程;
(2)求BC边上的垂直平分线所在直线方程;
(3)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com