
| A. | [$\frac{5}{12}$,$\frac{11}{6}$] | B. | (-∞,$\frac{5}{12}$]∪[$\frac{11}{6}$,+∞) | C. | [$\frac{20}{3}$,$\frac{37}{3}$] | D. | (-∞,$\frac{20}{3}$]∪[$\frac{37}{3}$,+∞) |
分析 a>0,b2=ac,可得c>0,b>0.由5b≥2(a+c),b=$\sqrt{ac}$,可得$2a-5\sqrt{ac}$+2c≤0,化为:$2(\sqrt{\frac{a}{c}})^{2}$-5$\sqrt{\frac{a}{c}}$+2≤0,令$\sqrt{\frac{a}{c}}$=t>0,即2t2-5t+2≤0,解得t范围.$\frac{5a+8b+4c}{a+b}$=$\frac{5a+8\sqrt{ac}+4c}{a+\sqrt{ac}}$=$\frac{5{t}^{2}+8t+4}{{t}^{2}+t}$=5+$\frac{3t+4}{{t}^{2}+t}$,再利用研究函数的单调性即可得出.
解答 解:∵a>0,b2=ac,∴c≥0.
当c=0时,b=0,不满足5b≥2(a+c),舍去.
∴c>0.
∵5b≥2(a+c),∴b>0.
由5b≥2(a+c),b=$\sqrt{ac}$,可得$2a-5\sqrt{ac}$+2c≤0,
化为:$2(\sqrt{\frac{a}{c}})^{2}$-5$\sqrt{\frac{a}{c}}$+2≤0,令$\sqrt{\frac{a}{c}}$=t>0,
即2t2-5t+2≤0,解得$\frac{1}{2}≤t≤2$.
∴$\frac{5a+8b+4c}{a+b}$=$\frac{5a+8\sqrt{ac}+4c}{a+\sqrt{ac}}$=$\frac{5\frac{a}{c}+8\sqrt{\frac{a}{c}}+4}{\frac{a}{c}+\sqrt{\frac{a}{c}}}$=$\frac{5{t}^{2}+8t+4}{{t}^{2}+t}$=$\frac{5({t}^{2}+t)+3t+4}{{t}^{2}+t}$=5+$\frac{3t+4}{{t}^{2}+t}$,
令f(t)=$\frac{3t+4}{{t}^{2}+t}$,t∈$[\frac{1}{2},2]$.
∴f′(t)=$\frac{-3{t}^{2}-8t-4}{({t}^{2}+t)^{2}}$<0,
∴函数f(t)在t∈$[\frac{1}{2},2]$内单调递减.
∴f(t)∈$[\frac{5}{3},\frac{22}{3}]$,
∴$\frac{5a+8b+4c}{a+b}$∈$[\frac{20}{3},\frac{37}{3}]$.
故选:C.
点评 本题考查了不等式的解法及其性质、利用导数研究函数的单调性极值与最值、换元方法,考查了推理能力与计算能力,属于难题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | f(1)<f(-1)<f(0) | B. | f(0)<f(1)<f(-1) | C. | f(-1)<f(0)<f(1) | D. | f(1)<f(0)<f(-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | ln2 | C. | 2ln2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{2}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
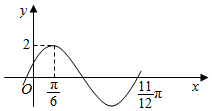 函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.
函数f(x)=2sin(ωx+φ)(ω>0,0<φ<π)的部分图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com