
【题目】在某大学自主招生考生中,所有选报Ⅱ类志向的考生全部参加了“数学与逻辑”和“阅读与表达”两个科目的考试,成绩分为A,B,C,D,E五个等级.某考场考生两科的考试成绩的数据统计如下图所示,其中“数学与逻辑”科目的成绩为B的考生有20人.
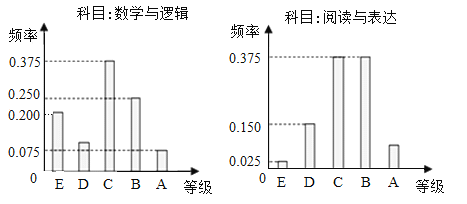
(1)求该考场考生中“阅读与表达”科目中成绩为A的人数;
(2)若等级A,B,C,D,E分别对应5分,4分,3分,2分,1分.
(i)求该考场考生“数学与逻辑”科目的平均分;
(ii)若该考场共有7人得分大于7分,其中有2人10分,2人9分,3人8分,从这7中随机抽取两人,求两人成绩之和大于等于18的概率.
【答案】(1)![]() (2)(i)
(2)(i)![]() (ii)
(ii)![]()
【解析】
(1)先计算出该考场共有80人,再根据![]() 求解;(2)(i)直接利用频率分布直方图中的平均数公式求该考场考生“数学与逻辑”科目的平均分;(ii)利用古典概型的概率求解.
求解;(2)(i)直接利用频率分布直方图中的平均数公式求该考场考生“数学与逻辑”科目的平均分;(ii)利用古典概型的概率求解.
(1)该考场共有![]() 人所以该考场考生中“阅读与表达”科目中成绩为A的人数为
人所以该考场考生中“阅读与表达”科目中成绩为A的人数为![]() .
.
(2)(i)该考场考生“数学与逻辑”科目的平均分为
![]()
![]()
(ii)设10分的人为A,B,9分的人为C,D,8分的为E,F,G,从中任意取两个人的基本事件有(A,B),(A,C),(A,D),(A,E),(A,F),(A,G), (B,C),(B,D),(B,E),(B,F),(B,G), (C,D),(C,E),(C,F),(C,G), (D,E),(D,F),(D,G), (E,F),(E,G),(F,G).共21个基本事件.
其中两人成绩之和大于等于18的基本事件有(A,B),(A,C),(A,D),(A,E),(A,F),(A,G), (B,C),(B,D), (B,E),(B,F),(B,G), (C,D),共12个基本事件.
由古典概型的概率得![]() .
.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() :
:![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,椭圆
,椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() .试判断
.试判断![]() 是否为定值?若是求出该定值,若不是定值,请说明理由.
是否为定值?若是求出该定值,若不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 过点
过点![]() ,焦点
,焦点![]() ,圆
,圆![]() 的直径为
的直径为![]() .
.
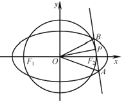
(1)求椭圆![]() 及圆
及圆![]() 的方程;
的方程;
(2)设直线![]() 与圆
与圆![]() 相切于第一象限内的点
相切于第一象限内的点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点.若
两点.若![]() 的面积为
的面积为![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周脾算经》有记载:一年有二十四个节气,每个节气晷(gui)长损益相同,晷是按照日影测定时刻的仪器,晷长即所测定的影子的长度,二十四节气及晷长变化如图所示,相邻两个节气晷长变化量相同,周而复始,若冬至晷长最长是一丈三尺五寸,夏至晷长最短是一尺五寸,(一丈等于10尺,一尺等于10寸),则秋分节气的晷长是( )
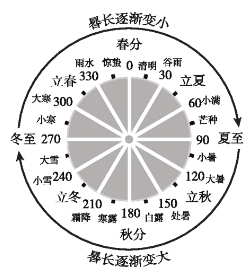
A.七尺五寸B.二尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】华为董事会决定投资开发新款软件,估计能获得![]() 万元到
万元到![]() 万元的投资收益,讨论了一个对课题组的奖励方案:奖金
万元的投资收益,讨论了一个对课题组的奖励方案:奖金![]() (单位:万元)随投资收益
(单位:万元)随投资收益![]() (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过![]() 万元,同时奖金不超过投资收益的
万元,同时奖金不超过投资收益的![]() .
.
(1)请分析函数![]() 是否符合华为要求的奖励函数模型,并说明原因;
是否符合华为要求的奖励函数模型,并说明原因;
(2)若华为公司采用模型函数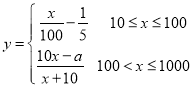 作为奖励函数模型,试确定正整数
作为奖励函数模型,试确定正整数![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知无穷数列![]() 的前
的前![]() 项和为
项和为![]() ,若对于任意的正整数
,若对于任意的正整数![]() ,均有
,均有![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .
.
(1)判断首项为![]() ,公比为
,公比为![]() 的无穷等比数列
的无穷等比数列![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(2)己知无穷数列![]() 具有性质
具有性质![]() ,且任意相邻四项之和都相等,求证:
,且任意相邻四项之和都相等,求证:![]() ;
;
(3)己知![]() ,数列
,数列![]() 是等差数列,
是等差数列,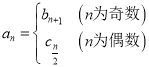 ,若无穷数列
,若无穷数列![]() 具有性质
具有性质![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(2)令![]() ,已知函数
,已知函数![]() 有两个极值点
有两个极值点![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若存在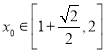 ,使不等式
,使不等式![]() 对任意
对任意![]() (取值范围内的值)恒成立,求实数
(取值范围内的值)恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的前n项和
的前n项和![]() ,且满足
,且满足![]() ,
,![]() ,数列
,数列![]() 是首项为2,公比为q(
是首项为2,公比为q(![]() )的等比数列.
)的等比数列.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设正整数k,t,r成等差数列,且![]() ,若
,若![]() ,求实数q的最大值;
,求实数q的最大值;
(3)若数列![]() 满足
满足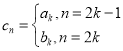 ,
,![]() ,其前n项和为
,其前n项和为![]() ,当
,当![]() 时,是否存在正整数m,使得
时,是否存在正整数m,使得![]() 恰好是数列
恰好是数列![]() 中的项?若存在,求岀m的值;若不存在,说明理由.
中的项?若存在,求岀m的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com