练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆 ： （ ）的离心率 ，直线 被以椭圆 的短轴为直径的圆截得的弦长为 .

    （1）求椭圆 的方程；

    （2）过点 的直线 交椭圆于 ， 两个不同的点，且 ，求 的取值范围.

    【答案】(1) ；(2) .

    【解析】试题分析：

    （1）由直线与圆的位置关系可得.由椭圆的离心率可得，则椭圆的方程为.

    （2）当直线的斜率为时， ，当直线的斜率不为时，设直线在y轴上的截距式方程为， ， ，联立方程可得，满足题意时，结合韦达定理可知，据此可知.综上可得.

    试题解析：

    （1）因为原点到直线的距离为，

    所以（），解得.

    又，得

    所以椭圆的方程为.

    （2）当直线的斜率为时， ，

    当直线的斜率不为时，设直线： ， ， ，

    联立方程组，得，

    由，得，

    所以，

    ，

    由，得，所以.

    综上可得： ，即.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为了进一步推动全市学习型党组织、学习型社会建设，某市组织开展“学习强国”知识测试，每人测试文化、经济两个项目，每个项目满分均为60分.从全体测试人员中随机抽取了100人，分别统计他们文化、经济两个项目的测试成绩，得到文化项目测试成绩的频数分布表和经济项目测试成绩的频率分布直方图如下：

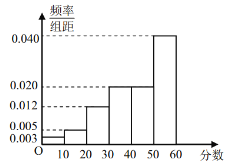
    经济项目测试成绩频率分布直方图

    分数区间

    频数

    2

    3

    5

    15

    40

    35

    文化项目测试成绩频数分布表

    将测试人员的成绩划分为三个等级如下：分数在区间内为一般，分数在区间内为良好，分数在区间内为优秀.

    （1）在抽取的100人中，经济项目等级为优秀的测试人员中女生有14人，经济项目等级为一般或良好的测试人员中女生有34人.填写下面列联表，并根据列联表判断是否有以上的把握认为“经济项目等级为优秀”与性别有关？

    优秀

    一般或良好

    合计

    男生数

    女生数

    合计

    （2）用这100人的样本估计总体，假设这两个项目的测试成绩相互独立.

    （i）从该市测试人员中随机抽取1人，估计其“文化项目等级高于经济项目等级”的概率.

    （ii）对该市文化项目、经济项目的学习成绩进行评价.

    附：

    0.150

    0.050

    0.010

    2.072

    3.841

    6.635

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在长方体中，，点E是棱上的一个动点，若平面交棱于点，给出下列命题：

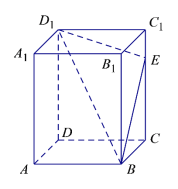
    ①四棱锥的体积恒为定值；

    ②存在点，使得平面；

    ③对于棱上任意一点，在棱上均有相应的点，使得平面；

    ④存在唯一的点，使得截面四边形的周长取得最小值.

    其中真命题的是____________．（填写所有正确答案的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂对一批产品进行了抽样检测.如图是根据抽样检测后的产品净重(单位：克)数据绘制的频率分布直方图，其中产品净重的范围是[96,106]，样本数据分组为[96,98)，[98,100)，[100,102)，[102,104)，[104,106]，已知样本中产品净重小于100克的个数是36.

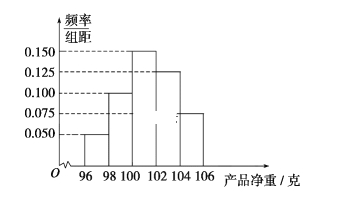
    (1)求样本容量及样本中净重大于或等于96克并且小于102克的产品的个数；

    (2)已知这批产品中每个产品的利润y(单位：元)与产品净重x(单位：克)的关系式为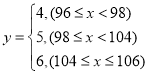求这批产品平均每个的利润.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱柱ABCD﹣A1B1C1D1中，底面四边形ABCD是矩形，平面DCC1D1⊥平面ABCD.AD=3，CD=DD1=5，∠D1DC=120°，M，N分别是线段AD1，BD的中点.

    （1）求证：MN//平面DCC1D1；

    （2）求证：MN⊥平面ADC1；

    （3）求三棱锥D1﹣ADC1的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校工会开展健步走活动，要求教职工上传3月1日至3月7日微信记步数信息，下图是职工甲和职工乙微信记步数情况：

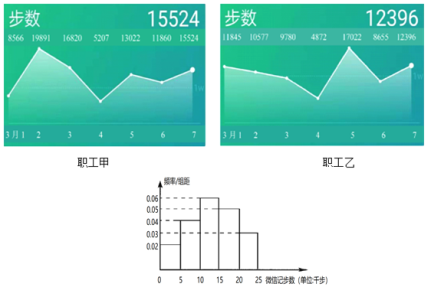
    （Ⅰ）从3月1日至3月7日中任选一天，求这一天职工甲和职工乙微信记步数都不低于10000的概率；

    （Ⅱ）从3月1日至3月7日中任选两天，记职工乙在这两天中微信记步数不低于10000的天数为，求 的分布列及数学期望；

    （Ⅲ）如图是校工会根据3月1日至3月7日某一天的数据，制作的全校200名教职工微信记步数的频率分布直方图．已知这一天甲和乙微信记步数在单位200名教职工中排名分别为第68和第142，请指出这是根据哪一天的数据制作的频率分布直方图（不用说明理由）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】定义集合与集合之差是由所有属于且不属于的元素组成的集合，记作 且．已知集合．

    （Ⅰ）若集合，写出集合的所有元素；

    （Ⅱ）从集合选出10个元素由小到大构成等差数列，其中公差的最大值和最小值分别是多少？公差为和的等差数列各有多少个？

    （Ⅲ）设集合,且集合中含有10个元素，证明：集合中必有10个元素组成等差数列．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】己知两点，，动点P在y轴上的摄影是H，且，

    （1）求动点P的轨迹方程；

    （2）设直线，的两个斜率存在，分别记为，，若，求点P的坐标；

    （3）若经过点的直线l与动点P的轨迹有两个交点为T、Q，当时，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《复仇者联盟4：终局之战》是安东尼·罗素和乔·罗素执导的美国科幻电影，改编自美国漫威漫画，自2019年4月24日上映以来票房火爆.某电影院为了解在该影院观看《复仇者联盟4》的观众的年龄构成情况，随机抽取了100名观众的年龄，并分成，，，，，，七组，得到如图所示的频率分布直方图.

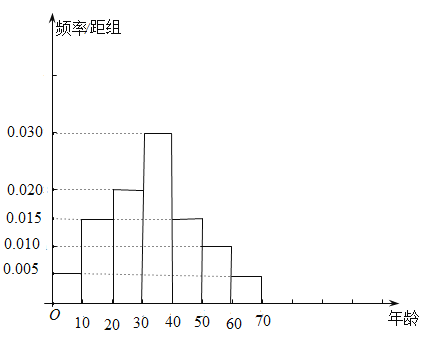
    （1）求这100名观众年龄的平均数（同一组数据用该区间的中点值作代表）、中位数；

    （2）该电影院拟采用抽奖活动来增加趣味性，观众可以选择是否参与抽奖活动（不参与抽奖活动按原价购票），活动方案如下：每张电影票价格提高10元，同时购买这样电影票的每位观众可获得3次抽奖机会，中奖1次则奖励现金元，中奖2次则奖励现金元，中奖三次则奖励现金元，其中且，已知观众每次中奖的概率均为.

    ①以某观众三次抽奖所获得的奖金总额的数学期望为评判依据，若要使抽奖方案对电影院有利，则最高可定为多少；

    ②据某时段内的统计，当时该电影院有600名观众选择参加抽奖活动，并且每增加1元，则参加抽奖活动的观众增加100人.设该时间段内观影的总人数不变，抽奖活动给电影院带来的利润的期望为，求的最大值.

    查看答案和解析>>

    同步练习册答案