
【题目】极坐标系的极点为直角坐标系的原点,极轴为x轴的正半轴,两坐标系中的单位长度相同,已知曲线C的极坐标方程为ρ=2(sinθ+cosθ).
(Ⅰ)求C的直角坐标方程;
(Ⅱ)直线 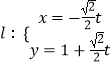 (t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
(t为参数)与曲线C交于A,B两点,与y轴交于E,求|EA|+|EB|的值.
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1=m,其前n项和为Sn , 且满足Sn+Sn+1=3n2+2n,若对n∈N+ , an<an+1恒成立,则m的取值范围是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,ABCD为直角梯形,AB∥CD,∠DAB=90°,四边形ADEF为等腰梯形,EF∥AD,已知AE⊥EC,AB=AF=EF=2,AD=CD=4.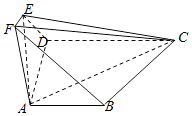
(1)求证:平面ABCD⊥平面ADEF;
(2)求直线CF与平面EAC所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
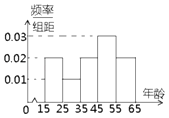
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”,为了了解人们对“延迟退休年龄政策”的态度,责成人社部进行调研,人社部从网上年龄在15~65岁的人群中随机调查100人,调查数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65] |
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
(1)由以上统计数据填2×2列联表,并判断是否95%的把握认为以45岁为界点的不同人群对“延迟退休年龄政策”的支持有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | |||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动,现从这8人中随机抽2人.
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率;
②记抽到45岁以上的人数为X,求随机变量X的分布列及数学期望.
P(K2≥k0) | 0.100 | 0.050 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)= ![]() x3+x2﹣3x,若方程|f(x)|2+t|f(x)|+1=0有12个不同的根,则实数t的取值范围为( )
x3+x2﹣3x,若方程|f(x)|2+t|f(x)|+1=0有12个不同的根,则实数t的取值范围为( )
A.(﹣ ![]() ,﹣2)
,﹣2)
B.(﹣∞,﹣2)
C.﹣ ![]() <t<﹣2
<t<﹣2
D.(﹣1,2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD的底面ABCD是平行四边形,侧面PAD是边长为2的正三角形,AB=BD= ![]() ,PB=3.
,PB=3.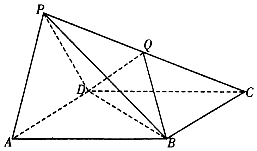
(1)求证:平面PAD⊥平面ABCD;
(2)设Q是棱PC上的点,当PA∥平面BDQ时,求二面角A﹣BD﹣Q的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在如图所示的多面体ABCDEF中,四边形ABCD为正方形,底面ABFE为直角梯形,∠ABF为直角, ![]() ,平面ABCD⊥平面ABFE.
,平面ABCD⊥平面ABFE.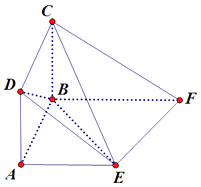
(1)求证:DB⊥EC;
(2)若AE=AB,求二面角C﹣EF﹣B的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com