
【题目】若函数f(x)=ax2-(3a-1)x+a2在[1,+∞)上是增函数,求实数a的取值范围.
【答案】0≤a≤1.
【解析】试题分析:先讨论参数a是否为0,若a=0,代入可得一次函数是增函数,成立;若a≠0,则二次函数开口向上,且x=1在对称轴的右侧,列出不等式解出a的范围即可.
试题解析:
①a=0时,f(x)=x在[1,+∞)上是增函数.
②a≠0时,∵f(x)在[1,+∞)上是增函数.
∴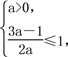 解得0<a≤1.
解得0<a≤1.
综上0≤a≤1.
点睛:本题考查一次函数和二次函数的单调性,属于基础题.根据函数解析式的形式,先要对最高次项的系数进行讨论,当a=0时,函数为一次函数,将a=0代入可知一次项系数为正,故为增函数;当a≠0时,函数为二次函数,若要使函数在[1,+∞)上是增函数,则需要开口向上,且[1,+∞)为增区间的子集,比较对称轴和1的大小关系列出不等式求解即可.


科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“幸”“福”“快”“乐”四个字,有放回地从中任取一个小球,取到“快”就停止,用随机模拟的方法估计直到第二次停止的概率:先由计算器产生1到4之间取整数值的随机数,且用1,2,3,4表示取出小球上分别写有“幸”“福”“快”“乐”四个字,以每两个随机数为一组,代表两次的结果,经随机模拟产生了20组随机数:
13 24 12 32 43 14 24 32 31 21
23 13 32 21 24 42 13 32 21 34
据此估计,直到第二次就停止的概率为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的左,右顶点分别为
的左,右顶点分别为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆交于
与椭圆交于![]() 两点,且
两点,且![]() 的面积是
的面积是![]() 的面积的3倍.
的面积的3倍.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() 与
与![]() 轴垂直,
轴垂直,![]() 是椭圆
是椭圆![]() 上位于直线
上位于直线![]() 两侧的动点,且满足
两侧的动点,且满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于![]() 四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
(1)求恰有1人申请![]() 片区房源的概率;
片区房源的概率;
(2)用![]() 表示选择
表示选择![]() 片区的人数,求
片区的人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两人玩掷骰子游戏,甲掷出的点数记为![]() ,乙掷出的点数记为
,乙掷出的点数记为![]() ,
,
若关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根时甲胜;方程有
有两个不相等的实数根时甲胜;方程有
两个相等的实数根时为“和”;方程没有实数根时乙胜.
(1)列出甲、乙两人“和”的各种情形;
(2)求甲胜的概率.
必要时可使用此表格

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2017届河南省郑州市第一中学高三上学期第一次质量检测数学(文)】已知函数![]() .
.
(1)证明:![]() ;
;
(2)若对任意![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com