
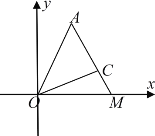
【题目】如图所示,在平面直角坐标系![]() 中,第一象限内有定点
中,第一象限内有定点![]() 和射线
和射线![]() ,已知
,已知![]() ,
,![]() 的倾斜角分别为
的倾斜角分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() 轴上的动点
轴上的动点![]() 与
与![]() ,
,![]() 共线.
共线.
(1)求![]() 点坐标(用
点坐标(用![]() 表示);
表示);
(2)求![]() 面积
面积![]() 关于
关于![]() 的表达式
的表达式![]() ;
;
(3)求![]() 面积的最小时直线
面积的最小时直线![]() 的方程.
的方程.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)由题易知![]() ,可得C点坐标;
,可得C点坐标;
(2)由题易知直线![]() , 设
, 设![]() ,
,![]() 共线,即斜率相等,可得
共线,即斜率相等,可得![]() ,再利用面积公式求得结果;
,再利用面积公式求得结果;
(3)由(2)易知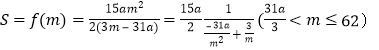 ,将分母看做关于
,将分母看做关于![]() 的二次函数,求最值即可得出结果.
的二次函数,求最值即可得出结果.
(1) ![]() ,又
,又![]()
(2)直线![]() ,设
,设![]() 共线,∴
共线,∴![]()
解得:![]() ,∴
,∴![]()
(3)法一、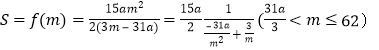
记![]()
(ⅰ)若![]() 即
即![]() ,函数
,函数![]() 在
在![]() 上递减,当且仅当
上递减,当且仅当![]() 即
即![]() 时
时
![]() 取得最小值,此时
取得最小值,此时![]() ,直线
,直线![]() 的方程为:
的方程为:![]()
(ⅱ)若![]() 即
即![]() ,函数
,函数![]() 在
在![]() 上递增,
上递增,![]() 上递减,当且仅当
上递减,当且仅当![]() 即
即![]() 时
时![]() 取得最小值,此时
取得最小值,此时![]() ,直线
,直线![]() 的方程为:
的方程为:![]()
法二、记![]() ,
,
![]()
以下用单调性的定义证明“对勾”函数的单调性(略)
(ⅰ)若![]() ,
,![]() ,
,![]() 在
在![]() 上递减,当且仅当
上递减,当且仅当
![]() 即
即![]() 时
时![]() 取得最小值,此时
取得最小值,此时![]() ,直线
,直线![]() 的方程为:
的方程为:![]()
(ⅱ)若![]() ,
,![]() ,
,![]() 在
在![]() 上递减, 在
上递减, 在![]() 上递增,
上递增,
当且仅当![]() 即
即![]() 时
时![]() 取得最小值,此时
取得最小值,此时![]() ,直线
,直线![]() 的方程为:
的方程为:![]() (法二中“对勾”函数的单调性未证明的不扣分)
(法二中“对勾”函数的单调性未证明的不扣分)


 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
【题目】随着网络营销和电子商务的兴起,人们的购物方式更具多样化.某调查机构随机抽取8名购物者进行采访,4名男性购物者中有3名倾向于网购,1名倾向于选择实体店,4名女性购物者中有2名倾向于选择网购,2名倾向于选择实体店.
(1)若从8名购物者中随机抽取2名,其中男女各一名,求至少1名倾向于选择实体店的概率:
(2)若从这8名购物者中随机抽取3名,设X表示抽到倾向于选择网购的男性购物者的人数,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】德国数学家科拉茨1937年提出了一个著名的猜想:任给一个正整数n,如果n是偶数,就将它减半(即![]() );如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
);如果n是奇数,则将它乘3加1(即3n+1),不断重复这样的运算,经过有限步后,一定可以得到1. 对于科拉茨猜想,目前谁也不能证明,也不能否定,现在请你研究:如果对正整数n(首项)按照上述规则施行变换后的第8项为1(注:l可以多次出现),则n的所有不同值的个数为
A. 4 B. 6 C. 8 D. 32
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点在直角坐标系的原点处,极轴与x轴的正半轴重合.直线l的参数方程为: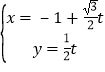 (t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(t为参数),曲线C的极坐标方程为:ρ=4cosθ.
(Ⅰ)写出C的直角坐标方程,并指出C是什么曲线;
(Ⅱ)设直线l与曲线C相交于P、Q两点,求|PQ|值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logm![]() (m>0且m≠1),
(m>0且m≠1),
(I)判断f(x)的奇偶性并证明;
(II)若m=![]() ,判断f(x)在(3,+∞)的单调性(不用证明);
,判断f(x)在(3,+∞)的单调性(不用证明);
(III)若0<m<1,是否存在β>α>0,使f(x)在[α,β]的值域为[logmm(β-1),logm(α-1)]?若存在,求出此时m的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AA1=AC=2AB=2,且BC1⊥A1C.
(Ⅰ)求证:平面ABC1⊥平面A1C1CA;
(Ⅱ)设D是A1C1的中点,判断并证明在线段BB1上是否存在点E,使DE∥平面ABC1;若存在,求三棱锥E﹣ABC1的体积.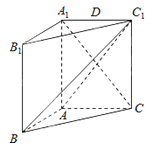
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}前n项和Sn满足Sn+1=a2Sn+a1 , 其中a2≠0.
(Ⅰ)求证数列{an}是首项为1的等比数列;
(Ⅱ)当a2=2时,是否存在等差数列{bn},使得a1bn+a2bn﹣1+a3bn﹣2+…+anb1=2n+1﹣n﹣2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线E:![]() ﹣
﹣![]() =1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
=1(a>0,b>0)的两条渐近线分别为l1:y=2x,l2:y=﹣2x.
(1)求双曲线E的离心率;
(2)如图,O为坐标原点,动直线l分别交直线l1 , l2于A,B两点(A,B分别在第一、第四象限),且△OAB的面积恒为8,试探究:是否存在总与直线l有且只有一个公共点的双曲线E?若存在,求出双曲线E的方程,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com