
【题目】如图,在正方体![]() 中,点
中,点![]() 是线段
是线段![]() 上的动点,则下列说法错误的是( )
上的动点,则下列说法错误的是( )
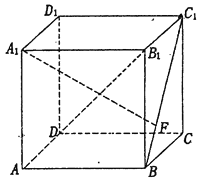
A. 无论点![]() 在
在![]() 上怎么移动,异面直线
上怎么移动,异面直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]()
B. 无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]()
C. 当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 与相交于一点,记为点
与相交于一点,记为点![]() ,且
,且![]()
D. 当点![]() 移动至
移动至![]() 中点时,直线
中点时,直线![]() 与平面
与平面![]() 所成角最大且为
所成角最大且为![]()
【答案】D
【解析】
结合正方体的结构特征及直线和平面的位置关系,对选项逐个分析即可选出答案。
对于A选项,设正方体棱长为1,连结![]() ,由于
,由于![]() ,故
,故![]() 就是直线
就是直线![]() 与
与![]() 所成角,假如
所成角,假如![]() ,则
,则![]() ,因为三角形
,因为三角形![]() 是边长为
是边长为![]() 的正三角形,高为
的正三角形,高为![]() ,所以
,所以![]() ,由于
,由于![]() ,故不成立,即直线
,故不成立,即直线![]() 与
与![]() 所成角都不可能是
所成角都不可能是![]() ,故A正确;
,故A正确;
对于B选项,连结![]() ,易知
,易知![]() ,且
,且![]() ,
,![]() ,则
,则![]() 平面
平面![]() ,故
,故![]() ,同理可证
,同理可证![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,由于
,由于![]() 在平面
在平面![]() 上,故无论点
上,故无论点![]() 在
在![]() 上怎么移动,都有
上怎么移动,都有![]() ,即选项B正确;
,即选项B正确;
对于C选项,易证![]() 和
和![]() 是正三棱锥,则
是正三棱锥,则![]() 和
和![]() 在平面
在平面![]() 的投影落在三角形
的投影落在三角形![]() 的重心,故当点
的重心,故当点![]() 移动至
移动至![]() 中点时,才有
中点时,才有![]() 与
与![]() 与相交于一点,记为点
与相交于一点,记为点![]() ,且
,且![]() ,即选项C正确;
,即选项C正确;
对于D选项,易证![]() 是正四面体,点
是正四面体,点![]() 在
在![]() 中点,设
中点,设![]() 在平面
在平面![]() 的投影为
的投影为![]() ,正四面体侧棱为
,正四面体侧棱为![]() ,直线
,直线![]() 与平面
与平面![]() 所成角
所成角![]() ,则
,则![]() ,
,![]() ,
,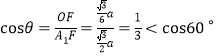 ,故
,故![]() ,即选项D不正确。
,即选项D不正确。
故选D.


科目:高中数学 来源: 题型:
【题目】如图,在正方体ABCD-A1B1C1D1中.
(I)求证:AC⊥BD1;
(Ⅱ)是否存在直线与直线AA1,CC1,BD1都相交?若存在,请你在图中画出两条满足条件的直线(不必说明画法及理由);若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某乡镇为了提高当地地方经济总量,决定引进资金对原有的两个企业![]() 和
和![]() 进行改造,计划每年对两个企业共投资500万元,要求对每个企业至少投资50万元.根据已有经验,改造后
进行改造,计划每年对两个企业共投资500万元,要求对每个企业至少投资50万元.根据已有经验,改造后![]() 企业的年收益
企业的年收益![]() (单位:万元)和
(单位:万元)和![]() 企业的年收益
企业的年收益![]() (单位:万元)与投入资金
(单位:万元)与投入资金![]() (单位:万元)分别满足关系式:
(单位:万元)分别满足关系式:![]() ,
,![]() .设对
.设对![]() 企业投资额为
企业投资额为![]() (单位:万元),每年两个企业的总收益为
(单位:万元),每年两个企业的总收益为![]() (单位:万元).
(单位:万元).
(1)求![]() ;
;
(2)试问如何安排两个企业的投入资金,才能使两个企业的年总收益达到最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】要得到函数y= ![]() cosx的图象,只需将函数y=
cosx的图象,只需将函数y= ![]() sin(2x+
sin(2x+ ![]() )的图象上所有的点的( )
)的图象上所有的点的( )
A.横坐标缩短到原来的 ![]() 倍(纵坐标不变),再向左平行移动
倍(纵坐标不变),再向左平行移动 ![]() 个单位长度
个单位长度
B.横坐标缩短到原来的 ![]() 倍(纵坐标不变),再向右平行移动
倍(纵坐标不变),再向右平行移动 ![]() 个单位长度
个单位长度
C.横坐标伸长到原来的2倍(纵坐标不变),再向左平行移动 ![]() 个单位长度
个单位长度
D.横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=2an+1(n∈N*).
(1)求数列{an}的通项公式;
(2)设Sn为数列{ ![]() }的前n项和,求证:1≤Sn<4.
}的前n项和,求证:1≤Sn<4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com