
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 过点
过点![]() ,其参数方程为
,其参数方程为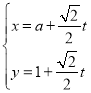 (
(![]() 为参数,
为参数,![]() ).以
).以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]()
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列四个命题:(1)一定存在直线![]() ,使函数
,使函数![]() 的图像与函数
的图像与函数![]() 的图像关于直线
的图像关于直线![]() 对称;(2)不等式:
对称;(2)不等式:![]() 的解集为
的解集为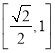 ;(3)已知数列
;(3)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,
,![]() ,则数列
,则数列![]() 一定是等比数列;(4)过抛物线
一定是等比数列;(4)过抛物线![]() 上的任意一点
上的任意一点![]() 的切线方程一定可以表示为
的切线方程一定可以表示为![]() .则正确命题的序号为_________________.
.则正确命题的序号为_________________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司欲对员工饮食习惯进行一次调查,从某科室的100人中的饮食结构调查结果统计如下表.
主食蔬菜 | 主食肉类 | 总计 | |
不超过45岁 | 15 | 40 | |
45岁以上 | 20 | ||
总计 |
(1)完成![]() 列联表,并判断能否有99%的把握认为员工的饮食习惯与年龄有关?
列联表,并判断能否有99%的把握认为员工的饮食习惯与年龄有关?
(2)在45岁以上员工中按照饮食习惯进行分层抽样抽出一个容量为6的样本,从这6个人中随机抽取3个人,求这3个人都主食蔬菜的概率.
附:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com