讨论函数y=cos(sinx)的定义域、值域、奇偶性、周期性、单调区间,并画出x∈[-π,π]的草图.
【答案】
分析:根据三角函数性质可得:①定义域:R ②值域:[cos1,1]
③奇偶性的判断可根据定义,检验f(-x)=cos(sin(-x)=cos(-sinx)=cos(sinx)=f(x),从而可判断
④根据周期的定义及三角函数性质检验f(x+π)=cos(sin(x+π)=cos(-sinx)=cos(sinx)=f(x),以π为周期的周期函数
⑤结合偶函数及π为周期可得单调减区间[
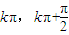
],单调增区间[
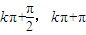
]
⑥x∈[-π,π]的图象可结合以上讨论的性质
解答:解:①定义域:R
②值域:[cos1,1]
③奇偶性:f(-x)=cos(sin(-x)=cos(-sinx)=cos(sinx)=f(x),为偶函数
④周期性:f(x+π)=cos(sin(x+π)=cos(-sinx)=cos(sinx)=f(x),以π为周期的周期函数
⑤单调区间:由图象易知:单调减区间[
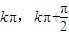
],单调增区间[
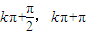
]
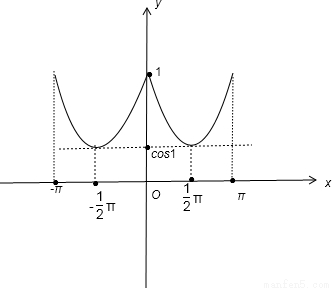
⑥x∈[-π,π]的简图如下
 点评:
点评:本题主要考查了三角函数的性质:三角函数的定义域,值域,函数的单调性,函数的奇偶性,函数的图象等知识的简单运用.

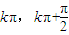 ],单调增区间[
],单调增区间[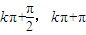 ]
]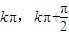 ],单调增区间[
],单调增区间[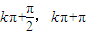 ]
]


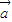 =(sin(ωx+ϕ),2),
=(sin(ωx+ϕ),2),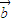 =(1,cos(ωx+ϕ))
=(1,cos(ωx+ϕ))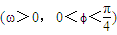 ,函数f(x)=(
,函数f(x)=(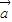 +
+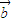 )•(
)•(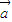 -
-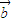 )的图象过点
)的图象过点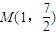 ,且该函数相邻两条对称轴间的距离为2.
,且该函数相邻两条对称轴间的距离为2.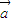 =
=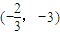 平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.
平移后,得到函数y=g(x)的图象,讨论函数y=g(x)在区间[1,2]上的单调性.