
【题目】一对父子参加一个亲子摸奖游戏,其规则如下:父亲在装有红色、白色球各两个的甲袋子里随机取两个球,儿子在装有红色、白色、黑色球各一个的乙袋子里随机取一个球,父子俩取球互相独立,两人各摸球一次合在一起称为一次摸奖,他们取出的三个球的颜色情况与他们获得的积分对应如下表:
所取球的情况 | 三个球均为红色 | 三个球均为不同色 | 恰有两球为红色 | 其他情况 |
所获得的积分 | 180 | 90 | 60 | 0 |
(1)求一次摸奖中,所取的三个球中恰有两个是红球的概率;
(2)设一次摸奖中,他们所获得的积分为![]() ,求
,求![]() 的分布列及均值(数学期望)
的分布列及均值(数学期望)![]() ;
;
(3)按照以上规则重复摸奖三次,求至少有两次获得积分为60的概率.
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]() ;(3)
;(3)![]() .
.
【解析】
试题分析:(1)所取三个球恰有两个是红球,包含两类基本事件,即父亲取出两个红球,儿子取出一个不是红球;父亲取出两球为一红一白,儿子取出一球为红球,然后利用古典概型概率计算公式及互斥事件的加法公式求得答案;(2)求出![]() 的取值,再求出取各个值的概,列出分布列,再由期望公式求期望;(3)由二项分布的定义知,三次摸奖中恰好获得
的取值,再求出取各个值的概,列出分布列,再由期望公式求期望;(3)由二项分布的定义知,三次摸奖中恰好获得![]() 个积分的次数
个积分的次数![]() ,然后结合互斥事件的概率公式求得答案.
,然后结合互斥事件的概率公式求得答案.
试题解析:
(1)设所取三个球恰有两个是红球为事件![]() ,则事件
,则事件![]() 包含两类基本事件:父亲取出两个红球,儿子取出一个不是红球,其概率
包含两类基本事件:父亲取出两个红球,儿子取出一个不是红球,其概率![]() ;
;
父亲取出两球为一红一白,儿子取出一球为红色,其概率为![]() ,
,
故![]() .
.
(2)![]() 可以取180,90,60,0,取各个值的概率分别为:
可以取180,90,60,0,取各个值的概率分别为:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所求分布列为:
| 180 | 90 | 60 | 0 |
|
|
|
|
|
随机变量![]() 的期望
的期望![]() .
.
(3)由二项分布的定义知,三次摸奖中恰好获得60个积分的次数![]() ,
,
则![]() ,
,
故所求概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x﹣a)2lnx,a∈R.
(I)若x=e是y=f(x)的极值点,求实数a的值;
(Ⅱ)若函数y=f(x)﹣4e2只有一个零点,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某服装厂每天的固定成本是30000元,每天最大规模的生产量是![]() 件.每生产一件服装,成本增加100元,生产
件.每生产一件服装,成本增加100元,生产![]() 件服装的收入函数是
件服装的收入函数是![]() ,记
,记![]() ,
,![]() 分别为每天生产
分别为每天生产![]() 件服装的利润和平均利润(
件服装的利润和平均利润(![]() ).
).
(1)当![]() 时,每天生产量
时,每天生产量![]() 为多少时,利润
为多少时,利润![]() 有最大值;
有最大值;
(2)每天生产量![]() 为多少时,平均利润
为多少时,平均利润![]() 有最大值,并求
有最大值,并求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() 与
与![]() 轴,
轴,![]() 轴的正半轴分别交于
轴的正半轴分别交于![]() 两点,原点
两点,原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,该椭圆的离心率为
,该椭圆的离心率为![]() .
.
(1)求椭圆的方程;
(2)过点![]() 的直线
的直线![]() 与椭圆交于两个不同的点
与椭圆交于两个不同的点![]() ,求线段
,求线段![]() 的垂直平分线在
的垂直平分线在![]() 轴上截距的取值范围.
轴上截距的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获![]() (单位:
(单位:![]() )与它的“相近”作物株数
)与它的“相近”作物株数![]() 之间的关系如下表所示:
之间的关系如下表所示:
| 1 | 2 | 3 | 4 |
| 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
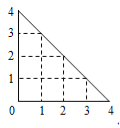
(1)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(2)在所种作物中堆积选取一株,求它的年收获量的分布列与数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com