
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计, 可以使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
参考解析
解析试题分析:假设角AMN的值为θ,由三角形AMN中角NAM为 .由正弦定理可得到AM的表达式,在三角形AMP中利用余弦定理表示出AP的值,由角θ的取值范围,再根据三角函数的单调性知识即可得到结论.本小题用了五种解法分别从三角,坐标系,圆等方面入手.
.由正弦定理可得到AM的表达式,在三角形AMP中利用余弦定理表示出AP的值,由角θ的取值范围,再根据三角函数的单调性知识即可得到结论.本小题用了五种解法分别从三角,坐标系,圆等方面入手.
解法一:设∠AMN=θ,在△AMN中,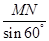 =
= .
.
因为MN=2,所以AM= sin(120°-θ). 2分
sin(120°-θ). 2分
在△APM中,cos∠AMP=cos(60°+θ). 4分
AP2=AM2+MP2-2 AM·MP·cos∠AMP= sin2(120°-θ)+4-2×2×
sin2(120°-θ)+4-2×2× sin(120°θ)cos(60°+θ) 6分
sin(120°θ)cos(60°+θ) 6分
= sin2(θ+60°)-
sin2(θ+60°)-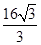 sin(θ+60°)cos(θ+60°)+4
sin(θ+60°)cos(θ+60°)+4
= [1-cos (2θ+120°)]-
[1-cos (2θ+120°)]-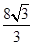 sin(2θ+120°)+4
sin(2θ+120°)+4
=- [
[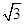 sin(2θ+120°)+cos (2θ+120°)]+
sin(2θ+120°)+cos (2θ+120°)]+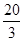
=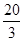 -
- sin(2θ+150°),θ∈(0,120°). 10分
sin(2θ+150°),θ∈(0,120°). 10分
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值2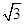 .
.
答:设计∠AMN为60°时,工厂产生的噪声对居民的影响最小. 12分
解法二(构造直角三角形):
设∠PMD=θ,在△PMD中,
∵PM=2,∴PD=2sinθ,MD=2cosθ. 2分
在△AMN中,∠ANM=∠PMD=θ,∴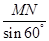 =
=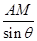 ,
,
AM= sinθ,∴AD=
sinθ,∴AD= sinθ+2cosθ,(θ≥
sinθ+2cosθ,(θ≥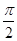 时,结论也正确). 4分
时,结论也正确). 4分
AP2=AD2+PD2=( sinθ+2cosθ)2+(2sinθ)2
sinθ+2cosθ)2+(2sinθ)2
= sin2θ+
sin2θ+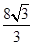 sinθcosθ+4cos2θ+4sin2θ 6分
sinθcosθ+4cos2θ+4sin2θ 6分
= ·
·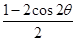 +
+ sin2θ+4=
sin2θ+4= sin2θ-
sin2θ- cos2θ+
cos2θ+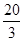
=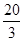 +
+ sin(2θ-
sin(2θ- ),θ∈(0,
),θ∈(0,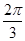 ). 10分
). 10分
当且仅当2θ- =
=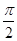 ,即θ=
,即θ= 时,AP2取得最大值12,即AP取得最大值2
时,AP2取得最大值12,即AP取得最大值2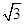 .
.
此时AM=AN=2,∠PAB=30° 12分
解法三:设AM=x,AN=y,∠AMN=α.
在△AMN中,因为MN=2,∠MAN=60°,
所以MN2=AM2+AN2-2 AM·AN·cos∠MAN,
即x2+y2-2xycos60°=x2+y2-xy=4. 2分
因为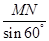 =
= ,即
,即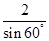 =
= ,
,
所以sinα= y,cosα=
y,cosα= =
= =
=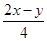 . 4分
. 4分
cos∠AMP=cos(α+60°)=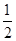 cosα-
cosα-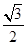 sinα=
sinα=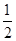


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案 期末好成绩系列答案
期末好成绩系列答案科目:高中数学 来源: 题型:解答题
如图,货轮在海上B处,以50海里/时的速度沿方位角(从正北方向顺时针转到目标方向线的水平角)为155o的方向航行,为了确定船位,在B点处观测到灯塔A的方位角为125o.半小时后,货轮到达C点处,观测到灯塔A的方位角为80o.求此时货轮与灯塔之间的距离(答案保留最简根号). 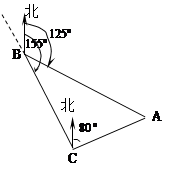
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,a,b,c分别是角A,B,C的对边,向量m=(2sinB,2-cos2B),n=(2sin2( +
+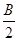 ),-1),且m⊥n.
),-1),且m⊥n.
(1)求角B的大小;
(2)求sinA+cosC的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
己知A、B、C分别为△ABC的三边a、b、c所对的角,向量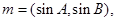
 ,且
,且 .
.
(1)求角C的大小:
(2)若sinA,sinC,sinB成等差数列,且 ,求边c的长.
,求边c的长.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(2013•重庆)在△ABC中,内角A、B、C的对边分别是a、b、c,且a2=b2+c2+ bc.
bc.
(1)求A;
(2)设a= ,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的最值.
,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的最值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com