
分析 (1)直接把给出的等式两边同时乘以$\frac{1}{i}$,然后利用复数的除法运算求得z1;
(2)设出复数z2,由z1•z2是纯虚数,则其实部等于0,虚部不等于0,联立后可求复数z2的实部,则复数z2可求.
解答 解:(Ⅰ)由z1•i=1+i,
得z1=$\frac{1+i}{i}$=$\frac{-i(1+i)}{-{i}^{2}}$=1-i;
(Ⅱ)∵z2的虚部为2,故设z2=m+2i (m∈R).
∵z1•z2=(1-i)(m+2i)=(m+2)+(2-m)i为纯虚数,
∴m+2=0,且2-m≠0,解得m=-2.
∴z2=-2+2i.
点评 本题考查了复数代数形式的乘除运算,考查了复数的有关定义,复数为纯虚数的条件是实部等于0虚部不等于0.是基础题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,-$\frac{2}{3}$]∪[2,+∞) | B. | [-$\frac{2}{3}$,2] | C. | [-$\frac{2}{3}$,0)∪(0,2] | D. | (-∞,0)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
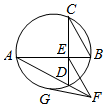 如图,E是圆内两弦AB和CD的交点,F为AD延长线上一点,FG切圆于G,且FE=FG.
如图,E是圆内两弦AB和CD的交点,F为AD延长线上一点,FG切圆于G,且FE=FG.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com