
【题目】已知函数![]() .
.
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围.
的取值范围.
【答案】(1) 当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;当
上单调递增;当![]() 时,函数
时,函数![]() 在区间
在区间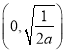 上单调递增,在区间
上单调递增,在区间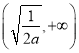 上单调递减(2)
上单调递减(2) ![]()
【解析】试题分析:(1)函数![]() 的定义域为
的定义域为![]() .
.![]() .对a分类讨论,明确函数的单调性;
.对a分类讨论,明确函数的单调性;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,即求
恒成立,即求![]() 的最小值大于等于零即可.
的最小值大于等于零即可.
试题解析:
(1)函数![]() 的定义域为
的定义域为![]() .
.
![]() .
.
①![]() 时,
时, ![]() ,故
,故![]() 在区间
在区间![]() 上单调递增;
上单调递增;
②当![]() 时,令
时,令![]() ,得
,得![]() ,
,
令![]() ,得
,得![]() ,
,
所以函数![]() 在区间
在区间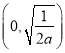 上单调递增,在区间
上单调递增,在区间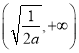 上单调递减.
上单调递减.
综上所述,当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上单调递增;
上单调递增;
当![]() 时,函数
时,函数![]() 在区间
在区间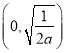 上单调递增,在区间
上单调递增,在区间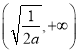 上单调递减.
上单调递减.
(2)当![]() 时,由(1),知函数
时,由(1),知函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以![]() ,所以
,所以![]() 恒成立,即
恒成立,即![]() 符合题意.
符合题意.
法一:当![]() 时,令
时,令![]() ,
,
解得: ![]() ,
,
令![]() ,解得
,解得![]() .
.
①当![]() 时,
时, ![]() ,
,
所以结合(1),知函数![]() 在区间
在区间 上单调递增,在区间
上单调递增,在区间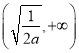 上单调递减,
上单调递减,
且![]()
![]() .
.
令![]() ,
,
![]() 恒成立,
恒成立,
又![]() ,
,
所以![]() 在区间
在区间![]() 上单调递增,
上单调递增,
所以存在![]() ,使得
,使得![]() ,
,
即存在![]() ,使得
,使得![]() ,
,
即当![]() 时,不符合题意.
时,不符合题意.
②当![]() 时,
时, ![]() ,
,
即![]() 在区间
在区间![]() 上恒成立,
上恒成立,
所以函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
所以![]() ,
,
显然![]() 不符合题意.
不符合题意.
综上所述,实数的取值范围为![]() .
.
法二:当![]() 时,令
时,令![]() ,
,
![]() ,
,
所以![]() ,取
,取![]() ,
,
故在![]() 上,
上, ![]()
![]() ,
,
不合题意,舍去.
综上所述,实数![]() 的取值范围为
的取值范围为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数) .
为实常数) .
(I)当![]() 时,求函数
时,求函数![]() 在
在![]() 上的最大值及相应的
上的最大值及相应的![]() 值;
值;
(II)当![]() 时,讨论方程
时,讨论方程![]() 根的个数.
根的个数.
(III)若![]() ,且对任意的
,且对任意的![]() ,都有
,都有 ,求
,求
实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 有两个平面互相平行,其余各面都是平行四边形的多面体是棱柱
B. 四棱锥的四个侧面都可以是直角三角形
C. 有两个平面互相平行,其余各面都是梯形的多面体是棱台
D. 棱台的各侧棱延长后不一定交于一点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sin2x﹣cos2x﹣2![]() sinxcosx(x∈R).
sinxcosx(x∈R).
(1)求f(x)的单调递增区间;
(2)求函数f(x)在区间[![]() ,
,![]() ]上的最大值和最小值.
]上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠BAD=![]() ,AB=BC=
,AB=BC=![]() AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.
AD=a,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到如图2中△A1BE的位置,得到四棱锥A1-BCDE.
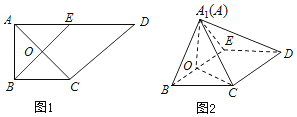
(Ⅰ)证明:CD⊥平面A1OC;
(Ⅱ)当平面A1BE⊥平面BCDE时,四棱锥A1-BCDE的体积为36![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】母线长为![]() ,底面半径为
,底面半径为![]() 的圆锥内有一球
的圆锥内有一球![]() ,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球
,与圆锥的侧面、底面都相切,现放入一些小球,小球与圆锥底面、侧面、球![]() 都相切,这样的小球最多可放入__________个.
都相切,这样的小球最多可放入__________个.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“既要金山银山,又要绿水青山”。某风景区在一个直径![]() 为
为![]() 米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点
米的半圆形花圆中设计一条观光线路。打算在半圆弧上任选一点![]() (与
(与![]() 不重合),沿
不重合),沿![]() 修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧
修一条直线段小路,在路的两侧(注意是两侧)种植绿化带;再沿弧![]() 修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。
修一条弧形小路,在小路的一侧(注意是一侧)种植绿化带,小路与绿化带的宽度忽略不计。

(1)设![]() (弧度),将绿化带的总长度表示为
(弧度),将绿化带的总长度表示为![]() 的函数
的函数![]() ;
;
(2)求绿化带的总长度![]() 的最大值。
的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由四个不同的数字![]() 1,2,4,
1,2,4,![]() 组成无重复数字的三位数.(最后的结果用数字表达)
组成无重复数字的三位数.(最后的结果用数字表达)
(Ⅰ)若![]() ,其中能被5整除的共有多少个?
,其中能被5整除的共有多少个?
(Ⅱ)若![]() ,其中能被3整除的共有多少个?
,其中能被3整除的共有多少个?
(Ⅲ)若![]() ,其中的偶数共有多少个?
,其中的偶数共有多少个?
(Ⅳ)若所有这些三位数的各位数字之和是252,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com