[题目]已知实数满足:有且仅有一个正方形.其四个顶点均在曲线上.试求这个正方形的面积. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知实数满足：有且仅有一个正方形，其四个顶点均在曲线上.试求这个正方形的面积.

【答案】

【解析】

由于曲线关于原点对称，所以该正方形的中心必过原点（否则，将这个正方形关于原点作对称又得到一个顶点均在曲线上的正方形）.

设正方形的一个顶点为，则、、是其他三个顶点.令的斜率分别为，则由，得，（1）

并且（由于在曲线上）有，（2）

（3）

由（2）、（3）得

. （4）

结合（1）得（5）

这说明方程（6）

有解.并且对（6）的任一解，结合（1）可求出（均为实数，因为）.再由（2）定出，它们满足（3）的第一个等式，由（5）有

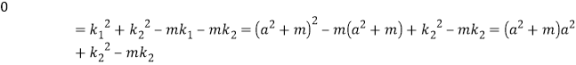
从而，（3）的第二个等式也成立.

确定的四点构成曲线上的正方形.

因为已知曲线上只有一个正方形，所以方程（6）只有两个相同的解.

由，得.

由（2）、（3）得.

故.从而.

则正方形的边长.

即正方形的面积.

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】企业需为员工缴纳社会保险，缴费标准是根据职工本人上一年度月平均工资（单位：元）的缴纳，

年份	2014	2015	2016	2017	2018
t	1	2	3	4	5
y	270	330	390	460	550

某企业员工甲在2014年至2018年各年中每月所撒纳的养老保险数额y（单位：元）与年份序号t的统计如下表：

（1）求出t关于t的线性回归方程；

（2）试预测2019年该员工的月平均工资为多少元？

附：回归直线的斜率和截距的最小二乘法估计公式分别为：

（注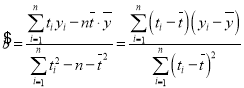：，，其中）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知空间几何体ABCDE中，△BCD与△CDE均是边长为2的等边三角形，△ABC是腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD.

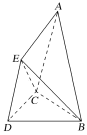
(1)试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出证明；

(2)求三棱锥E－ABC的体积.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下列说法正确的是（）

A. “，若，则且”是真命题

B. 在同一坐标系中，函数与的图象关于轴对称．

C. 命题“，使得”的否定是“，都有”

D. ，“”是“”的充分不必要条件

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】对数函数g（x）=1ogax（a＞0，a≠1）和指数函数f（x）=ax（a＞0，a≠1）互为反函数．已知函数f（x）=3x，其反函数为y=g（x）．

（Ⅰ）若函数g（kx2+2x+1）的定义域为R，求实数k的取值范围；

（Ⅱ）若0＜x1＜x2且|g（x1）|=|g（x2）|，求4x1+x2的最小值；

（Ⅲ）定义在I上的函数F（x），如果满足：对任意x∈I，总存在常数M＞0，都有-M≤F（x）≤M成立，则称函数F（x）是I上的有界函数，其中M为函数F（x）的上界．若函数h（x）=，当m≠0时，探求函数h（x）在x∈[0，1]上是否存在上界M，若存在，求出M的取值范围，若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】下面给出三个游戏，袋子中分别装有若干只有颜色不同的小球（大小，形状，质量等均一样），从袋中无放回地取球，则其中不公平的游戏是______.

	游戏1	游戏2	游戏3
球数	3个黑球和一个白球	一个黑球和一个白球	2个黑球和2个白球
取法	取1个球，再取1个球	取1个球	取1个球，再取1个球
胜利规则	取出的两个球同色→甲胜	取出的球是黑球→甲胜	取出的两个球同色→甲胜
胜利规则	取出的两个球不同色→乙胜	取出的球是白球→乙胜	取出的两个球不同色→乙胜