考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,
(1)z的几何意义为区域内点到原点的距离.
(2)z的几何意义为区域内的点与定点M(-2,0)的斜率.
(3)设m=3x+4y+3,利用目标函数的几何意义,利用数形结合确定m的取值范围即可得到结论.
解答:
解:作出不等式组对应的平面区域如图:(阴影部分ABC).
由
,解得
,即A(5,2),
由
,解得
,即B(1,
)
由
,解得
,即C(1,1)
(1)z=
的几何意义为区域内点到原点的距离,
由图象可知OC的距离最小,OA的距离最大,
即最大值为z=
=,最小值为z=
=.
(2)z=
的几何意义为区域内的点与定点M(-2,0)的斜率,
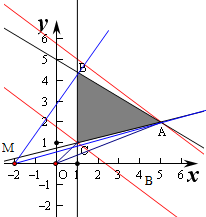
由图象知MB的斜率最大,MA的斜率最小,
即z的最大值为z=
=,最小值为z=
=.
(3)设m=3x+4y+3得y=
-x+,此时z=|m|,
平移直线y=
-x+,
由图象可知当直线y=
-x+经过点A时,直线y=
-x+的截距最大,此时m最大.
当直线y=
-x+经过点C时,直线y=
-x+的截距最小,此时m最小.
代入目标函数m=3x+4y+3=3+4+3=10,
代入目标函数m=3x+4y+3=15+8+3=26,
即10≤m≤26,
则10≤|m|≤26,即10≤z≤26,
则z=|3x+4y+3|的最大值为26,最小值为10.
点评:本题主要考查线性规划的应用,综合考查目标函数的几何意义,利用距离,斜率和截距的几何意义是解决线性规划的基本方法.




 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案