
【题目】已知函数![]() .
.
(I)求函数f(x)的单调区间;
(Ⅱ)若不等式![]() 对任意的
对任意的![]() 都成立(其中e是自然对数的底数),求
都成立(其中e是自然对数的底数),求![]() 的最大值.
的最大值.
【答案】(I)增区间![]() ,减区间
,减区间![]() ;(I)
;(I)![]() .
.
【解析】
(I)求导数![]() ,由于
,由于![]() 分母为正,因此对分子(设其为
分母为正,因此对分子(设其为![]() )再求导,以确定正负,
)再求导,以确定正负,![]() 仍不能确定其零点、极值、正负,因此再一次求导,可确定出
仍不能确定其零点、极值、正负,因此再一次求导,可确定出![]() 的最值与单调性,从而可确定
的最值与单调性,从而可确定![]() 的单调性与零点,最终可确定
的单调性与零点,最终可确定![]() 的单调区间;
的单调区间;
(II)分离常数,得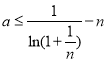 ,为此求出函数
,为此求出函数![]() 在
在![]() 上的最小值.这可利用导数知识求解.
上的最小值.这可利用导数知识求解.
函数![]() 的定义域是
的定义域是![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
![]() 时,
时,![]() ,
,![]() 在
在![]() 上为增函数,
上为增函数,
![]() 时,
时,![]() ,
,![]() 在
在![]() 上为减函数,
上为减函数,
∴![]() 在
在![]() 处取得极大值,而
处取得极大值,而![]() ,
,
∴![]() ,函数
,函数![]() 在
在![]() 上为减函数.
上为减函数.
于是当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
∴当![]() 时,
时,![]() ,
,![]() 为增函数,
为增函数,
当![]() 时,
时,![]() ,
,![]() 为减函数,
为减函数,
故函数![]() 的增区间为
的增区间为![]() ,减区间为
,减区间为![]() .
.
(II)不等式![]() 等价于不等式
等价于不等式![]() ,由
,由![]() 可得:
可得:
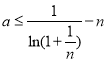 ,
,
设![]() ,
,![]() ,
,
则![]() ,
,
由(I)知![]() ,即
,即![]()
∴![]()
![]() ,
,![]() ,于是
,于是![]() 在
在![]() 上为减函数,
上为减函数,
故函数![]() 在
在![]() 上的最小值为
上的最小值为![]() ,
,
所以![]() 的最大值为
的最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知函数![]() ,下列命题:
,下列命题:
①![]() 的定义域为
的定义域为![]() ;
;
②![]() 是奇函数;
是奇函数;
③![]() 在
在![]() 上单调递增;
上单调递增;
④若实数![]() 满足
满足![]() ,则
,则![]() ;
;
⑤设函数![]() 在上的最大值为
在上的最大值为![]() ,最小值为
,最小值为![]() ,则
,则![]() .
.
其中真命题的序号是______.(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着新政策的实施,海淘免税时代于2016年4月8日正式结束,新政策实施后,海外购物的费用可能会增加.为了解新制度对海淘的影响,某网站调查了喜欢海淘的1000名网友,其态度共有两类:第一类是会降低海淘数量,共有400人,第二类是不会降低海淘数量,共有600人,若从这1000人中按照分层抽样的方法抽取10人后进行打分,其打分的茎叶图如下图所示,图中有数据缺失,但已知“第一类”和“第二类”网民打分的均值相等,则“第一类”网民打分的方差为( )
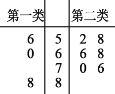
A.159B.179C.189D.209
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学生自主创业,经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润800元,未售出的产品,每
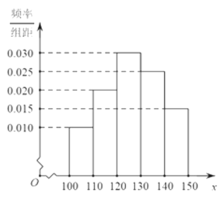
该产品获利润800元,未售出的产品,每![]() 亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了
亏损200元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.该大学生为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (单位:
(单位:![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量,![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于94000元的概率;
不少于94000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的均值.
的均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4,坐标系与参数方程
已知曲线![]() ,直线
,直线![]() :
:![]() (
(![]() 为参数).
为参数).
(I)写出曲线![]() 的参数方程,直线
的参数方程,直线![]() 的普通方程;
的普通方程;
(II)过曲线![]() 上任意一点
上任意一点![]() 作与
作与![]() 夹角为
夹角为![]() 的直线,交
的直线,交![]() 于点
于点![]() ,
,![]() 的最大值与最小值.
的最大值与最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了200位高三学生的成绩进行统计分析得到如图所示频率分布直方图:
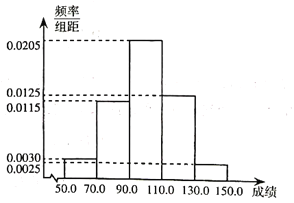
(1)计算这些学生成绩的平均值![]() 及样本方差
及样本方差![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)由频率分布直方图认为,这次成绩X近似服从正态分布![]() ,其中μ近似为样本平均数
,其中μ近似为样本平均数![]() ,
,![]() 近似为样本方差
近似为样本方差![]() .
.
(i)求![]() ;
;
(ii)从高三学生中抽取10位学生进行面批,记![]() 表示这10位学生成绩在
表示这10位学生成绩在![]() 的人数,利用(i)的结果,求数学期望
的人数,利用(i)的结果,求数学期望![]() .
.
附:![]() ;
;
若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 的图象为C,下面结论正确的是( )
的图象为C,下面结论正确的是( )
A.函数f(x)的最小正周期是2π.
B.函数f(x)在区间![]() 上是递增的
上是递增的
C.图象C关于点![]() 对称
对称
D.图象C由函数g(x)=sin2x的图象向左平移![]() 个单位得到
个单位得到
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}满足:对任意n∈N*,均有an=bn+cn成立,且{bn},{cn}都是等比数列,则称(bn,cn)是数列{an}的一个等比拆分.
(1)若an=2n,且(bn,bn+1)是数列{an}的一个等比拆分,求{bn}的通项公式;
(2)设(bn,cn)是数列{an}的一个等比拆分,且记{bn},{cn}的公比分别为q1,q2;
①若{an}是公比为q的等比数列,求证:q1=q2=q;
②若a1=1,a2=2,q1q2=﹣1,且对任意n∈N*,an+13<anan+1an+2+an+2﹣an恒成立,求a3的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com