【题目】如图，已知长方体的长和宽都是
cm，高是4 cm.
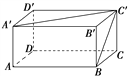
(1)求BC和A′C′所成的角的度数．
(2)求AA′和BC′所成的角的度数．
【答案】（1）
；（2）
【解析】试题分析：（1）根据长方体的性质可得
，所以
为
与
所成的角，由正方形的性质可得
，从而可得结果；（2）长方体中， 
，所以
为
与
所成的角，利用直角三角形的性质可得
，所以
与
所成的角为
.
试题解析：(1)在长方体中，BC∥B′C′，所以∠A′C′B′为BC与A′C′所成的角，因为A′B′＝B′C′＝
cm，∠A′B′C′＝90°，所以∠A′C′B′＝45°，所以BC和A′C′所成的角为45°.
(2)在长方体中，AA′∥BB′，所以∠C′BB′为AA′与BC′所成的角，因为BB′＝4 cm，B′C′＝
cm，所以∠C′BB′＝60°，所以AA′和BC′所成的角为60°.
科目：高中数学 来源： 题型：
【题目】已知圆
： 
过椭圆
： 
(
)的短轴端点， 
， 
分别是圆
与椭圆
上任意两点，且线段
长度的最大值为3．
（Ⅰ）求椭圆
的方程；
（Ⅱ）过点
作圆
的一条切线交椭圆
于
， 
两点，求
的面积的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】学校艺术节对同一类的
，
，
，
四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：
甲说：“是或作品获得一等奖”；
乙说：“作品获得一等奖”；
丙说：“，两项作品未获得一等奖”；
丁说：“是作品获得一等奖”.
若这四位同学中只有两位说的话是对的，则获得一等奖的作品是__________．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学举办安全法规知识竞赛，从参赛的高一、高二学生中各抽出100人的成绩作为样本，对高一年级的100名学生的成绩进行统计，并按
， 
， 
， 
， 
， 
分组，得到成绩分布的频率分布直方图（如图）。
（1）若规定60分以上（包括60分）为合格，计算高一年级这次竞赛的合格率；
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此，估计高一年级这次知识竞赛的学生的平均成绩；
（3）若高二年级这次竞赛的合格率为
，由以上统计数据填写下面
列联表，并问是否有
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
附：参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知三条直线l1：2x-y+a =" 0" (a＞0)，直线l2：-4x+2y+1 = 0和直线l3：x+y-1= 0，且l1与l2的距离是
．
（1）求a的值；
（2）能否找到一点P，使得P点同时满足下列三个条 件：
①P是第一象限的点；
②P 点到l1的距离是P点到l2的距离的
；
③P点到l1的距离与P点到l3的距离之比是
∶
．若能，求P点坐标；若不能，说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以直角坐标系的原点
为极点， 
轴的正半轴为极轴，并在两种坐标系中取相同的长度单位，点
的极坐标为
，圆
以
为圆心，4为半径；又直线
的极坐标方程为
。
（Ⅰ）求直线
和圆
的普通方程；
（Ⅱ）试判定直线
和圆
的位置关系．若相交，则求直线
被圆
截得的弦长．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝3ax2＋2bx＋c，a＋b＋c＝0，f(0)>0，f(1)>0，证明a>0，并利用二分法证明方程f(x)＝0在区间[0,1]内有两个实根．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某校学生研究性学习小组发现，学生上课的注意力指标随着听课时间的变化而变化，老师讲课开始时，学生的兴趣激增；接下来学生的兴趣将保持较理想的状态一段时间，随后学生的注意力开始分散．设 
表示学生注意力指标，该小组发现 
随时间 
（分钟）的变化规律（
越大，表明学生的注意力越集中）如下： 
（
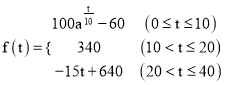，且 
）
若上课后第 
分钟时的注意力指标为 
，回答下列问题：
（1）求 
的值；
（2）上课后第 
分钟时和下课前 
分钟时比较，哪个时间注意力更集中?并请说明理由．
（3）在一节课中，学生的注意力指标至少达到 
的时间能保持多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
