
【题目】《周易》是我国古代典籍,用“卦”描述了天地世间万象变化.如图是一个八卦图,包含乾、坤、震、巽、坎、离、艮、兑八卦(每一卦由三个爻组成,其中“![]() ”表示一个阳爻,“
”表示一个阳爻,“![]() ”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )
”表示一个阴爻).若从八卦中任取两卦,这两卦的六个爻中恰有一个阳爻的概率为( )

A.![]() B.
B.![]()
C.![]() D.
D.![]()
科目:高中数学 来源: 题型:
【题目】某工厂为了提高生产效率,对生产设备进行了技术改造,为了对比技术改造后的效果,采集了技术改造前后各20次连续正常运行的时间长度(单位:天)数据,整理如下:
改造前:19,31,22,26,34,15,22,25,40,35,18,16,28,23,34,15,26,20,24,21
改造后:32,29,41,18,26,33,42,34,37,39,33,22,42,35,43,27,41,37,38,36
(1)完成下面的列联表,并判断能否有99%的把握认为技术改造前后的连续正常运行时间有差异?
超过30 | 不超过30 | |
改造前 | ||
改造后 |
(2)工厂的生产设备的运行需要进行维护,工厂对生产设备的生产维护费用包括正常维护费,保障维护费两种.对生产设备设定维护周期为T天(即从开工运行到第kT天,k∈N*)进行维护.生产设备在一个生产周期内设置几个维护周期,每个维护周期相互独立.在一个维护周期内,若生产设备能连续运行,则只产生一次正常维护费,而不会产生保障维护费;若生产设备不能连续运行,则除产生一次正常维护费外,还产生保障维护费.经测算,正常维护费为0.5万元/次;保障维护费第一次为0.2万元/周期,此后每增加一次则保障维护费增加0.2万元.现制定生产设备一个生产周期(以120天计)内的维护方案:T=30,k=1,2,3,4.以生产设备在技术改造后一个维护周期内能连续正常运行的频率作为概率,求一个生产周期内生产维护费的分布列及均值.
附: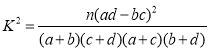
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )过点
)过点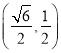 ,离心率为
,离心率为![]() .其左、右焦点分别为
.其左、右焦点分别为![]() ,
,![]() ,O为坐标原点.直线l:
,O为坐标原点.直线l:![]() 与以线段
与以线段![]() 为直径的圆相切,且直线l与椭圆C交于不同的A,B两点.
为直径的圆相切,且直线l与椭圆C交于不同的A,B两点.
(1)求椭圆C的方程;
(2)若满足![]() ,求
,求![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C方程为![]() ,椭圆中心在原点,焦点在x轴上.
,椭圆中心在原点,焦点在x轴上.
(1)证明圆C恒过一定点M,并求此定点M的坐标;
(2)判断直线![]() 与圆C的位置关系,并证明你的结论;
与圆C的位置关系,并证明你的结论;
(3)当![]() 时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线
时,圆C与椭圆的左准线相切,且椭圆过(1)中的点M,求此时椭圆方程;在x轴上是否存在两定点A,B使得对椭圆上任意一点Q(异于长轴端点),直线![]() ,
,![]() 的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
的斜率之积为定值?若存在,求出A,B坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示的多面体ABCDEF满足:正方形ABCD与正三角形FBC所在的两个平面互相垂直,FB∥AE且FB=2EA.
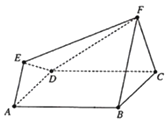
(1)证明:平面EFD⊥平面ABFE;
(2)求二面角E﹣FD﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际上通常用年龄中位数指标作为划分国家或地区人口年龄构成的标准:年龄中位数在20岁以下为“年轻型”人口;年龄中位数在20~30岁为“成年型”人口;年龄中位数在30岁以上为“老龄型”人口.

如图反映了我国全面放开二孩政策对我国人口年龄中位数的影响.据此,对我国人口年龄构成的类型做出如下判断:①建国以来直至2000年为“成年型”人口;②从2010年至2020年为“老龄型”人口;③放开二孩政策之后我国仍为“老龄型”人口.其中正确的是( )
A.②③B.①③C.②D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,且原点到直线
,且原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若不经过点![]() 的直线
的直线![]() :
:![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且与圆
两点,且与圆![]() 相切.试探究
相切.试探究![]() 的周长是否为定值,若是,求出定值;若不是,请说明理由.
的周长是否为定值,若是,求出定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆E:![]() +
+![]() =1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为
=1(a>b>0)的左、右焦点分别为F1,F2,过点F1的直线交椭圆E于A,B两点.若椭圆E的离心率为![]() ,三角形ABF2的周长为4
,三角形ABF2的周长为4![]() .
.
(1)求椭圆E的方程;
(2)设不经过椭圆的中心而平行于弦AB的直线交椭圆E于点C,D,设弦AB,CD的中点分别为M,N,证明:O,M,N三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com