
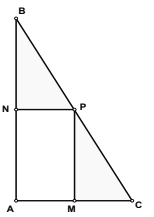
【题目】我校为丰富师生课余活动,计划在一块直角三角形![]() 的空地上修建一个占地面积为
的空地上修建一个占地面积为![]() (平方米)的
(平方米)的![]() 矩形健身场地,如图,点
矩形健身场地,如图,点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 上,且
上,且![]() 点在斜边
点在斜边![]() 上,已知
上,已知![]() ,
, ![]() 米,
米, ![]() 米,
米, ![]() .设矩形
.设矩形![]() 健身场地每平方米的造价为
健身场地每平方米的造价为![]() 元,再把矩形
元,再把矩形![]() 以外(阴影部分)铺上草坪,每平方米的造价为
以外(阴影部分)铺上草坪,每平方米的造价为![]() 元(
元(![]() 为正常数)
为正常数)
(1)试用![]() 表示
表示![]() ,并求
,并求![]() 的取值范围;
的取值范围;
(2)求总造价![]() 关于面积
关于面积![]() 的函数
的函数![]() ;
;
(3)如何选取![]() ,使总造价
,使总造价![]() 最低(不要求求出最低造价)
最低(不要求求出最低造价)
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:

(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“过大年,吃水饺”是我国不少地方过春节的一大习俗,2018年春节前夕,![]() 市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.
市某质检部门随机抽取了100包某种品牌的速冻水饺,检测其某项质量指标.

(1)求所抽取的100包速冻水饺该项质量指标值的样本平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(2)①由直方图可以认为,速冻水饺的该项质量指标值![]() 服从正态分布
服从正态分布![]() ,利用该正态分布,求
,利用该正态分布,求![]() 落在
落在![]() 内的概率;
内的概率;
②将频率视为概率,若某人从某超市购买了4包这种品牌的速冻水饺,记这4包速冻水饺中这种质量指标值位于![]() 内的包数为
内的包数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:①计算得所抽查的这100包速冻水饺的质量指标的标准差为![]() ;
;
②若![]() ,则
,则![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地![]() 户家庭的年收入
户家庭的年收入![]() (万元)和年饮食支出
(万元)和年饮食支出![]() (万元)的统计资料如下表:
(万元)的统计资料如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的线性回归方程;(结果保留到小数点后
的线性回归方程;(结果保留到小数点后![]() 为数字)
为数字)
(2)利用(1)中的回归方程,分析这![]() 户家庭的年饮食支出的变化情况,并预测该地年收入
户家庭的年饮食支出的变化情况,并预测该地年收入![]() 万元的家庭的年饮食支出.(结果保留到小数点后
万元的家庭的年饮食支出.(结果保留到小数点后![]() 位数字)
位数字)
附:回归直线的斜率和截距的最小二乘法估计公式分别为:
 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四棱锥![]() ,
, ![]() 平面
平面![]() ,底面
,底面![]() 中,
中, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为
为![]() 的中点.
的中点.

(1)求证:平面![]() 平面
平面![]() ;
;
(2)问在棱![]() 上是否存在点
上是否存在点![]() ,使
,使![]() 平面
平面![]() ,若存在,请求出二面角
,若存在,请求出二面角![]() 的余弦值;若不存在,请说明理由.
的余弦值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com