
【题目】在△ABC中, ![]() .
.
(1)求tanA;
(2)若BC=1,求ACAB的最大值,并求此时角B的大小.
【答案】
(1)
解:由正弦定理知 ![]() ,
,
即 ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵0<A<π,
∴ ![]()
(2)
解:在△ABC中,BC2=AC2+AB2﹣2ACABcosA,且BC=1,
∴1=AC2+AB2﹣ACAB,
∵AC2+AB2≥2ACAB,
∴1≥2ACAB﹣ACAB,
即ACAB≤1,当且仅当AC=AB=1时,ACAB取得最大值1,
此时 ![]()
【解析】(1)由正弦定理化简已知可得 ![]() ,利用三角函数恒等变换的应用进一步化简可得
,利用三角函数恒等变换的应用进一步化简可得 ![]() ,结合范围0<A<π,即可得解.(2)由已知及余弦定理可得1=AC2+AB2﹣ACAB,利用基本不等式解得ACAB≤1,从而得解.
,结合范围0<A<π,即可得解.(2)由已知及余弦定理可得1=AC2+AB2﹣ACAB,利用基本不等式解得ACAB≤1,从而得解.
【考点精析】本题主要考查了正弦定理的定义和余弦定理的定义的相关知识点,需要掌握正弦定理:![]() ;余弦定理:
;余弦定理:![]() ;
;![]() ;
;![]() 才能正确解答此题.
才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】某小型工厂安排甲、乙两种产品的生产,已知工厂生产甲、乙两种产品每吨所需要的原材料A,B,C的数量和一周内可用资源数量如下表所示:
原材料 | 甲(吨) | 乙(吨) | 资源数量(吨) |
A | 1 | 1 | 50 |
B | 4 | 0 | 160 |
C | 2 | 5 | 200 |
如果甲产品每吨的利润为300元,乙产品每吨的利润为200元,那么适当安排生产后,工厂每周可获得的最大利润为______元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角三角形ABC中,角A,B,C的对边分别为a,b,c,已知sinA= ![]() ,tan(A﹣B)=﹣
,tan(A﹣B)=﹣ ![]() .
.
(1)求tanB的值;
(2)若b=5,求c.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱柱ABCD﹣A1B1C1D1的底面ABCD为正方形,AA1⊥AC,M、N分别为棱AA1、CC1的中点.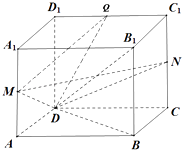
(1)求证:直线MN⊥平面B1BD;
(2)已知AA1=AB,AA1⊥AB,取线段C1D1的中点Q,求二面角Q﹣MD﹣N的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x3-3ax+b(a≠0).
(1)若曲线y=f(x)在点(2,f(2))处与直线y=8相切,求a,b的值;
(2)求函数f(x)的单调区间与极值点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产甲,乙两种芯片,其质量按测试指标划分为:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种芯片各100件进行检测,检测结果统计如表:
测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
芯片甲 | 8 | 12 | 40 | 32 | 8 |
芯片乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计芯片甲,芯片乙为合格品的概率;
(2)生产一件芯片甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件芯片乙,若是合格品可盈利50元,若是次品则亏损10元.在(I)的前提下,
(i)记X为生产1件芯片甲和1件芯片乙所得的总利润,求随机变量X的分布列和数学期望;
(ii)求生产5件芯片乙所获得的利润不少于140元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项为﹣6的等差数列{an}的前7项和为0,等比数列{bn}满足b3=a7 , |b3﹣b4|=6.
(1)求数列{bn}的通项公式;
(2)是否存在正整数k,使得数列{ ![]() }的前k项和大于
}的前k项和大于 ![]() ?并说明理由.
?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com