
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() ,
,![]() ,试证:
,试证:![]() .
.
【答案】(1)单调增区间为![]() 与
与![]() ,减区间为
,减区间为![]() ;(2)见解析
;(2)见解析
【解析】
(1)求导,令![]() ,可得增区间,令
,可得增区间,令![]() ,可得减区间,要注意函数定义域为
,可得减区间,要注意函数定义域为![]() ;
;
(2)构造函数![]() ,
,![]() ,求导后得,
,求导后得,![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增,利用函数的单调性可得
上单调递增,利用函数的单调性可得![]() 在
在![]() 上恒成立,因为
上恒成立,因为![]() ,所以
,所以![]() ,即
,即![]() ①;同理,构造函数
①;同理,构造函数![]() ,
,![]() ,可证
,可证![]() ②,结合①②,结论可证.
②,结合①②,结论可证.
(1)由题设知函数![]() 的定义域为
的定义域为![]() 且
且![]()
故当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以![]() 的单调增区间为
的单调增区间为![]() 与
与![]() ,减区间为
,减区间为![]() ;
;
(2)由(1)知:![]() ,先证
,先证![]() .
.
构造函数![]() ,
,![]()
则![]()
故![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增
上单调递增
所以![]() 在
在![]() 上恒成立,
上恒成立,
又![]() ,得
,得![]() ,又
,又![]() 且函数
且函数![]() 在
在![]() 上单调递减
上单调递减
故![]() ,即
,即![]() ①
①
再证![]() .构造函数
.构造函数![]() ,
,![]()
![]()
故![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上单调递增
上单调递增
所以![]() 在
在![]() 上恒成立,
上恒成立,
又![]() ,得
,得![]() ,
,
又![]() 且函数
且函数![]() 在
在![]() 上单调递增
上单调递增
故![]() ,即
,即![]() ②
②
结合①②得:![]()


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】“移动支付、高铁、网购、共享单车”被称为中国的“新四大发明”.为了帮助50岁以上的中老年人更快地适应“移动支付”,某机构通过网络组织50岁以上的中老年人学习移动支付相关知识.学习结束后,每人都进行限时答卷,得分都在![]() 内.在这些答卷(有大量答卷)中,随机抽出
内.在这些答卷(有大量答卷)中,随机抽出![]() 份,统计得分绘出频率分布直方图如图.
份,统计得分绘出频率分布直方图如图.
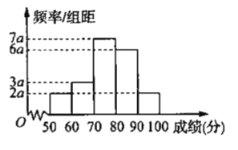
(1)求出图中![]() 的值,并求样本中,答卷成绩在
的值,并求样本中,答卷成绩在![]() 上的人数;
上的人数;
(2)以样本的频率为概率,从参加这次答卷的人群中,随机抽取![]() 名,记成绩在
名,记成绩在![]() 分以上(含
分以上(含![]() 分)的人数为
分)的人数为![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着科学技术的飞速发展,网络也已经逐渐融入了人们的日常生活,网购作为一种新的消费方式,因其具有快捷、商品种类齐全、性价比高等优势而深受广大消费者认可.某网购公司统计了近五年在本公司网购的人数,得到如下的相关数据(其中“x=1”表示2015年,“x=2”表示2016年,依次类推;y表示人数):
x | 1 | 2 | 3 | 4 | 5 |
y(万人) | 20 | 50 | 100 | 150 | 180 |
(1)试根据表中的数据,求出y关于x的线性回归方程,并预测到哪一年该公司的网购人数能超过300万人;
(2)该公司为了吸引网购者,特别推出“玩网络游戏,送免费购物券”活动,网购者可根据抛掷骰子的结果,操控微型遥控车在方格图上行进. 若遥控车最终停在“胜利大本营”,则网购者可获得免费购物券500元;若遥控车最终停在“失败大本营”,则网购者可获得免费购物券200元. 已知骰子出现奇数与偶数的概率都是![]() ,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从
,方格图上标有第0格、第1格、第2格、…、第20格。遥控车开始在第0格,网购者每抛掷一次骰子,遥控车向前移动一次.若掷出奇数,遥控车向前移动一格(从![]() 到
到![]() )若掷出偶数遥控车向前移动两格(从
)若掷出偶数遥控车向前移动两格(从![]() 到
到![]() ),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第
),直到遥控车移到第19格胜利大本营)或第20格(失败大本营)时,游戏结束。设遥控车移到第![]() 格的概率为
格的概率为![]() ,试证明
,试证明![]() 是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
是等比数列,并求网购者参与游戏一次获得免费购物券金额的期望值.
附:在线性回归方程![]() 中,
中,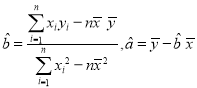 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年1月6日,中国物流与采购联合会正式发布了中国仓储指数,中国仓储指数是反映仓储行业经营和国内市场主要商品供求状况与变化趋势的一套指数体系,如图所示的折线图是2019年甲企业和乙企业的仓储指数走势情况.根据该折线图,下列结论中不正确的是( )
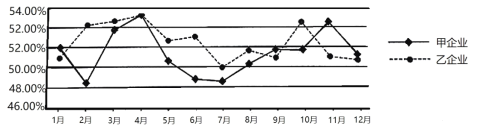
A.2019年1月至4月甲企业的仓储指数比乙企业的仓储指数波动大
B.甲企业2019年的年平均仓储指数明显低于乙企业2019年的年平均仓储指数
C.两企业2019年的最大仓储指数都出现在4月份
D.2019年7月至9月乙企业的仓储指数的增幅高于甲企业
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是定义在
是定义在![]() 上的函数,若对任何实数
上的函数,若对任何实数![]() 以及
以及![]() 中的任意两数
中的任意两数![]() 、
、![]() ,恒有
,恒有![]() ,则称
,则称![]() 为定义在
为定义在![]() 上的
上的![]() 函数.
函数.
(1)证明函数![]() 是定义域上的
是定义域上的![]() 函数;
函数;
(2)判断函数![]() 是否为定义域上的
是否为定义域上的![]() 函数,请说明理由;
函数,请说明理由;
(3)若![]() 是定义域为
是定义域为![]() 的函数,且最小正周期为
的函数,且最小正周期为![]() ,试证明
,试证明![]() 不是
不是![]() 上的
上的![]() 函数.
函数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】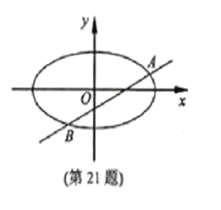
(本题满分15分)已知m>1,直线![]() ,
,
椭圆![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点.
的左、右焦点.
(Ⅰ)当直线![]() 过右焦点
过右焦点![]() 时,求直线
时,求直线![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() ,
,
![]() 的重心分别为
的重心分别为![]() .若原点
.若原点![]() 在以线段
在以线段
![]() 为直径的圆内,求实数
为直径的圆内,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com