
【题目】已知函数f(x)=lnx﹣ ![]() ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
ax2+(1﹣a)x,其中a∈R,f(x)的导函数是f′(x).
(1)求函数f(x)的极值;
(2)在曲线y=f(x)的图象上是否存在不同的两点A(x1 , y1),B(x2 , y2)(x1≠x2),使得直线AB的斜率k=f′( ![]() )?若存在,求出x1与x2的关系;若不存在,请说明理由.
)?若存在,求出x1与x2的关系;若不存在,请说明理由.
【答案】
(1)解:由已知得,f′(x)= ![]() (1)当a≤0时,∵x>0,∴f′(x)>0;
(1)当a≤0时,∵x>0,∴f′(x)>0;
∴f(x)在(0,+∞)上是增函数,此时函数f(x)无极值;(2)当a>0时, ![]() ;
;
∴当x ![]() 时,g′(x)>0;当x
时,g′(x)>0;当x ![]() 时,g′(x)<0;
时,g′(x)<0;
∴函数f(x)在 ![]() 上是增函数,在
上是增函数,在 ![]() 上是减函数;
上是减函数;
∴当 ![]() 时,f(x)有极大值
时,f(x)有极大值 ![]() ,无极小值;
,无极小值;
综上所述,当a≤0时,函数f(x)无极值,当a>0时,f(x)有极大值 ![]() ,无极小值.
,无极小值.
(2)解:由题意得,
![]() =
= 
=  =
= 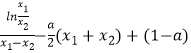 .
.
![]() .
.
由 ![]() 得,
得, 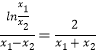 ;
;
即 ![]() ,即
,即 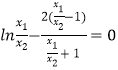 ;
;
令 ![]() ,不妨设x1>x2,则t>1,记
,不妨设x1>x2,则t>1,记 ![]() ;
;
![]() ,所以g(t)在(1,+∞)上是增函数;
,所以g(t)在(1,+∞)上是增函数;
所以g(t)>g(1)=0,所以方程g(t)=0无解,则满足条件的两点A,B不存在.
【解析】(1)求导数 ![]() ,讨论a的符号,这样便可判断导数的符号,从而可判断每种情况是否存在极值,若存在便可求出该极值;(2)先根据条件求出斜率
,讨论a的符号,这样便可判断导数的符号,从而可判断每种情况是否存在极值,若存在便可求出该极值;(2)先根据条件求出斜率 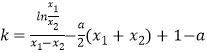 ,而可得到
,而可得到 ![]() ,这样便可根据条件得出
,这样便可根据条件得出 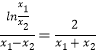 ,然后换元
,然后换元 ![]() ,并设x1>x2 , t>1,从而得出
,并设x1>x2 , t>1,从而得出 ![]() ;求导数并可判断导数符号g′(t)>0,从而g(t)>g(1),而g(1)=0,这即说明g(t)=0无解,从而得出满足条件的两点A,B不存在.
;求导数并可判断导数符号g′(t)>0,从而g(t)>g(1),而g(1)=0,这即说明g(t)=0无解,从而得出满足条件的两点A,B不存在.
【考点精析】认真审题,首先需要了解函数的极值与导数(求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值).
是极小值).


科目:高中数学 来源: 题型:
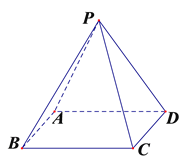
【题目】如图在四棱锥P-ABCD中,底面ABCD为矩形,侧面PAD![]() 底面ABCD,
底面ABCD, ![]() ;
;
(1)求证:平面PAB![]() 平面PCD;
平面PCD;
(2)若过点B的直线![]() 垂直平面PCD,求证:
垂直平面PCD,求证: ![]() //平面PAD.
//平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2﹣4|x|+3,x∈R.
(1)判断函数的奇偶性并将函数写成分段函数的形式;
(2)画出函数的图象,根据图象写出它的单调区间; 
(3)若函数f(x)的图象与y=a的图象有四个不同交点,则实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个口袋装有大小相同的小球9个,其中红球2个、黑球3个、白球4个,现从中抽取2次,每次抽取一个球.
(1)若有放回地抽取2次,求两次所取的球的颜色不同的概率;
(2)若不放回地抽取2次,取得红球记2分,取得黑球记1分,取得白球记0分,记两次取球的得分之和为随机变量X,求X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《汉字听写大会》不断创收视新高,为了避免“书写危机”弘扬传统文化,某市对全市10万名市民进行了汉字听写测试,调查数据显示市民的成绩服从正态分布![]() .现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组
.现从某社区居民中随机抽取50名市民进行听写测试,发现被测试市民正确书写汉字的个数全部在160到184之间,将测试结果按如下方式分成六组:第一组![]() ,第二组
,第二组![]() ,…,第六组
,…,第六组![]() ,如图是按上述分组方法得到的频率分布直方图.
,如图是按上述分组方法得到的频率分布直方图.
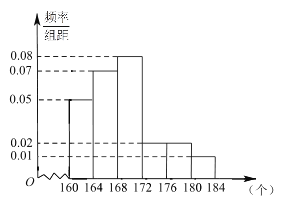
(1)试评估该社区被测试的50名市民的成绩在全市市民中成绩的平均状况及这50名市民成绩在172个以上(含172个)的人数;
(2)在这50名市民中成绩在172个以上(含172个)的人中任意抽取2人,该2人中成绩排名(从高到低)在全市前130名的人数记为![]() ,求
,求![]() 的数学期望.
的数学期望.
参考数据:若![]() ~
~![]() ,则
,则![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)如果对于任意的![]() ,
, ![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)设函数![]() ,
, ![]() ,过点
,过点![]() 作函数
作函数![]() 的图象的所有切线,令各切点的横坐标按从小到大构成数列
的图象的所有切线,令各切点的横坐标按从小到大构成数列![]() ,求数列
,求数列![]() 的所有项之和的值.
的所有项之和的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
中,AE⊥DE,CD⊥平面ADE,AB⊥平面ADE,CD=DA=6,AB=2,DE=3.
(1)求![]() 到平面
到平面![]() 的距离
的距离
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com