
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为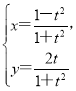 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求C上的点到![]() 距离的最大值.
距离的最大值.
【答案】(1)C的普通方程为![]() .
.![]() 的直角坐标方程为
的直角坐标方程为![]() (2)3
(2)3
【解析】
(1)把曲线C的参数方程平方相加可得普通方程,把x=ρcosθ,y=ρsinθ代入ρcosθ![]() ρsinθ+4=0,可得直线l的直角坐标方程;
ρsinθ+4=0,可得直线l的直角坐标方程;
(2)设出椭圆上动点的坐标(参数形式),再由点到直线的距离公式写出距离,利用三角函数求最值.
(1)由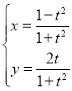 (t为参数),因为
(t为参数),因为![]() ,且
,且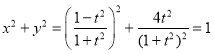 ,
,
所以C的普通方程为![]() .
.
由ρcosθ![]() ρsinθ+4=0,得x
ρsinθ+4=0,得x![]() y+4=0.
y+4=0.
即直线l的直角坐标方程为得x![]() y+4=0;
y+4=0;
(2)由(1)可设C的参数方程为![]() (
(![]() 为参数,
为参数,![]() ).
).
则P到直线得x![]() y+4=0的距离为:
y+4=0的距离为:
C上的点到![]() 的距离为
的距离为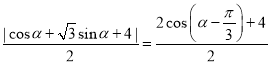 .
.
当![]() 时,
时,![]() 取得最大值6,故C上的点到
取得最大值6,故C上的点到![]() 距离的最大值为3.
距离的最大值为3.


科目:高中数学 来源: 题型:
【题目】某企业在“精准扶贫”行动中,决定帮助一贫困山区将水果运出销售.现有8辆甲型车和4辆乙型车,甲型车每次最多能运6吨且每天能运4次,乙型车每次最多能运10吨且每天能运3次,甲型车每天费用320元,乙型车每天费用504元.若需要一天内把180吨水果运输到火车站,则通过合理调配车辆,运送这批水果的费用最少为( )
A.2400元B.2560元C.2816元D.4576元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】凤鸣山中学的高中女生体重![]() (单位:kg)与身高
(单位:kg)与身高![]() (单位:cm)具有线性相关关系,根据一组样本数据
(单位:cm)具有线性相关关系,根据一组样本数据![]() (
(![]() ),用最小二乘法近似得到回归直线方程为
),用最小二乘法近似得到回归直线方程为![]() ,则下列结论中不正确的是( )
,则下列结论中不正确的是( )
A.![]() 与
与![]() 具有正线性相关关系
具有正线性相关关系
B.回归直线过样本的中心点![]()
C.若该中学某高中女生身高增加1cm,则其体重约增加0.85kg
D.若该中学某高中女生身高为160cm,则可断定其体重必为50.29kg.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将数列![]() 的前
的前![]() 项分成两部分,且两部分的项数分别是
项分成两部分,且两部分的项数分别是![]() ,若两部分和相等,则称数列
,若两部分和相等,则称数列![]() 的前
的前![]() 项的和能够进行
项的和能够进行![]() 等和分割.
等和分割.
(1)若![]() ,试写出数列
,试写出数列![]() 的前
的前![]() 项和所有等和分割;
项和所有等和分割;
(2)求证:等差数列![]() 的前
的前![]() 项的和能够进行
项的和能够进行![]() 等和分割;
等和分割;
(3)若数列![]() 的通项公式为:
的通项公式为:![]() ,且数列
,且数列![]() 的前
的前![]() 项的和能够进行等和分割,求所有满足条件的
项的和能够进行等和分割,求所有满足条件的![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,函数
,函数![]()
(1)若![]() ,求出函数
,求出函数![]() 在区间上
在区间上![]() 的最大值.
的最大值.
(2)若![]() ,求出函数
,求出函数![]() 的单调区间(不必证明)
的单调区间(不必证明)
(3)若存在![]() ,使得关于
,使得关于![]() 方程
方程![]() 有三个不相等的实数根,求出实数
有三个不相等的实数根,求出实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线C的参数方程为
中,曲线C的参数方程为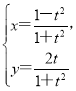 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求C的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)求C上的点到![]() 距离的最大值.
距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,
,![]() ,求
,求![]() 的值域;
的值域;
(2)当![]() 时,求
时,求![]() 的最小值
的最小值![]() ;
;
(3)是否存在实数![]() 、
、![]() ,同时满足下列条件:①
,同时满足下列条件:① ![]() ;② 当
;② 当![]() 的定义域为
的定义域为![]() 时,其值域为
时,其值域为![]() .若存在,求出
.若存在,求出![]() 、
、![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列六个命题:
(1)若![]() ,则函数
,则函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(2)![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(3)![]() 的反函数与
的反函数与![]() 是相同的函数.
是相同的函数.
(4)![]() 无最大值也无最小值.
无最大值也无最小值.
(5)![]() 的最小正周期为
的最小正周期为![]() .
.
(6)![]() 有对称轴两条,对称中心有三个.
有对称轴两条,对称中心有三个.
则正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com