
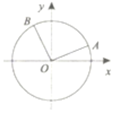
 如图,在平面直角坐标系xOy中,以O为角的顶点,x轴正半轴为始边的角α、β的终边分别与单位圆交于点A,B,若点A的横坐标是$\frac{4}{5}$,点B的纵坐标是$\frac{\sqrt{3}}{2}$.
如图,在平面直角坐标系xOy中,以O为角的顶点,x轴正半轴为始边的角α、β的终边分别与单位圆交于点A,B,若点A的横坐标是$\frac{4}{5}$,点B的纵坐标是$\frac{\sqrt{3}}{2}$.分析 (1)利用条件求得A、B的坐标,再利用两角差的余弦公式求得cos(α-β)的值.
(2)根据 $\overrightarrow{OA}$与$\overrightarrow{OB}$夹角的余弦值cosθ=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=$\overrightarrow{OA}$•$\overrightarrow{OB}$,计算求的结果.
解答 解:由题意可知点A的纵坐标为$\sqrt{{1-(\frac{4}{5})}^{2}}$=$\frac{3}{5}$,∴点A($\frac{4}{5}$,$\frac{3}{5}$).
点B的横坐标为-$\sqrt{{1-(\frac{\sqrt{3}}{2})}^{2}}$=-$\frac{1}{2}$,∴点B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
所以,根据三角函数的定义可知,sinα=$\frac{3}{5}$,cosα=$\frac{4}{5}$,sinβ=$\frac{\sqrt{3}}{2}$,cosβ=-$\frac{1}{2}$,
(1)cos(α-β)=cosαcosβ+sinαsinβ=$\frac{4}{5}$•(-$\frac{1}{2}$)+$\frac{3}{5}$•$\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}-4}{10}$.
(2)因为$\overrightarrow{OA}$=($\frac{4}{5}$,$\frac{3}{5}$),$\overrightarrow{OB}$=(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
故 $\overrightarrow{OA}$与$\overrightarrow{OB}$夹角的余弦值cosθ=$\frac{\overrightarrow{OA}•\overrightarrow{OB}}{|\overrightarrow{OA}|•|\overrightarrow{OB}|}$=$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{4}{5}$•(-$\frac{1}{2}$)+$\frac{3}{5}$•$\frac{\sqrt{3}}{2}$=$\frac{-4+3\sqrt{3}}{10}$.
点评 本题主要考查同角三角函数的基本关系,用两个向量的数量积表示两个向量的夹角,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
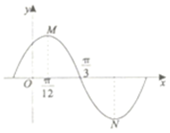 若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是这段图象的最高点与最低点,且OM⊥ON,则A=( )
若函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)在一个周期内的图象如图所示,M,N分别是这段图象的最高点与最低点,且OM⊥ON,则A=( )| A. | $\frac{π}{6}$ | B. | $\frac{\sqrt{7}π}{12}$ | C. | $\frac{\sqrt{7}π}{6}$ | D. | $\frac{\sqrt{7}π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
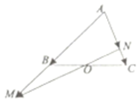 如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=m$\overrightarrow{AN}$,则m的值为$\frac{7}{5}$.
如图所示,在△ABC中,点O是BC的中点,过点O的直线分别交直线AB,AC于不同的两点M,N,若$\overrightarrow{AB}$=$\frac{3}{5}$$\overrightarrow{AM}$,$\overrightarrow{AC}$=m$\overrightarrow{AN}$,则m的值为$\frac{7}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com