
【题目】如图所示,在正方体ABCD﹣A1B1C1D1中,E是棱DD1的中点.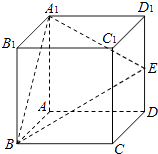
(1)求直线BE与平面ABB1A1所成的角的正弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
【答案】
(1)解:如图(a),取AA1的中点M,连接EM,BM,因为E是DD1的中点,四边形ADD1A1为正方形,所以EM∥AD.
又在正方体ABCD﹣A1B1C1D1中.AD⊥平面ABB1A1,所以EM⊥面ABB1A1,从而BM为直线BE在平面ABB1A1上的射影,
∠EBM直线BE与平面ABB1A1所成的角.
设正方体的棱长为2,则EM=AD=2,BE= ![]() ,
,
于是在Rt△BEM中, ![]()
即直线BE与平面ABB1A1所成的角的正弦值为 ![]() .
.
(2)解:在棱C1D1上存在点F,使B1F平面A1BE,
事实上,如图(b)所示,分别取C1D1和CD的中点F,G,连接EG,BG,CD1,FG,
因A1D1∥B1C1∥BC,且A1D1=BC,所以四边形A1BCD1为平行四边形,
因此D1C∥A1B,又E,G分别为D1D,CD的中点,所以EG∥D1C,从而EG∥A1B,这说明A1,B,G,E共面,所以BG平面A1BE
因四边形C1CDD1与B1BCC1皆为正方形,F,G分别为C1D1和CD的中点,所以FG∥C1C∥B1B,且FG=C1C=B1B,因此四边形B1BGF为平行四边形,所以B1F∥BG,而B1F平面A1BE,BG平面A1BE,故B1F∥平面A1BE.
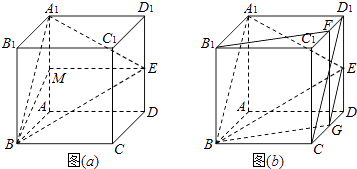
【解析】(1)先取AA1的中点M,连接EM,BM,根据中位线定理可知EM∥AD,而AD⊥平面ABB1A1 , 则EM⊥面ABB1A1 , 从而BM为直线BE在平面ABB1A1上的射影,则∠EBM直线BE与平面ABB1A1所成的角,设正方体的棱长为2,则EM=AD=2,BE=3,于是在Rt△BEM中,求出此角的正弦值即可.(2)在棱C1D1上存在点F,使B1F平面A1BE,分别取C1D1和CD的中点F,G,连接EG,BG,CD1 , FG,因A1D1∥B1C1∥BC,且A1D1=BC,所以四边形A1BCD1为平行四边形,根据中位线定理可知EG∥A1B,从而说明A1 , B,G,E共面,则BG面A1BE,根据FG∥C1C∥B1G,且FG=C1C=B1B,从而得到四边形B1BGF为平行四边形,则B1F∥BG,而B1F平面A1BE,BG平面A1BE,根据线面平行的判定定理可知B1F∥平面A1BE.
【考点精析】本题主要考查了直线与平面平行的判定和空间角的异面直线所成的角的相关知识点,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则 才能正确解答此题.
才能正确解答此题.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:高中数学 来源: 题型:
【题目】已知命题p:函数f(x)=|2x+3c|在[-1,+∞)上单调递增;命题q:函数g(x)=![]() +2有零点.
+2有零点.
(1)若命题p和q均为真命题,求实数c的取值范围;
(2)是否存在实数c,使得p∧(q)是真命题?若存在,求出c的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,公园内有一块边长为![]() 的等边
的等边![]() 形状的三角地,现修成草坪,图中
形状的三角地,现修成草坪,图中![]() 把草坪分成面积相等的两部分,
把草坪分成面积相等的两部分,![]() 在
在![]() 上,
上,![]() 在
在![]() 上.
上.
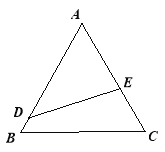
(Ⅰ)设![]()
![]() ,试用
,试用![]() 表示
表示![]() 的函数关系式;
的函数关系式;
(Ⅱ)如果![]() 是灌溉水管,为节约成本希望它最短,
是灌溉水管,为节约成本希望它最短,![]() 的位置应该在哪里?如果
的位置应该在哪里?如果![]() 是参观线路,则希望它最长,
是参观线路,则希望它最长,![]() 的位置又在哪里?请给予证明.
的位置又在哪里?请给予证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点M(x,y)到直线ι:x=4的距离是它到点N(1,0)的距离的2倍.
(1)求动点M的轨迹C的方程;
(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求点A的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P﹣ABCD中,底面ABCD为矩形,PA⊥平面PDC,E为棱PD的中点.
(1)求证:PB∥平面EAC;
(2)求证:平面PAD⊥平面ABCD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,位于A处的信息中心获悉:在其正东方向相距40海里的B处有一艘渔船遇险,在原地等待营救.信息中心立即把消息告知在其南偏西30°,相距20海里的C处的乙船,现乙船朝北偏东![]() 的方向即沿直线CB前往B处救援,则
的方向即沿直线CB前往B处救援,则![]() 等于 ( )
等于 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱柱ABCD﹣A1B1C1D1中,A1A⊥底面ABCD,四边形ABCD为梯形,AD∥BC,且AD=2BC,过A1、C、D三点的平面记为α,BB1与α的交点为Q.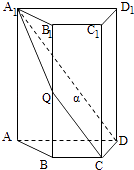
(1)证明:Q为BB1的中点;
(2)若AA1=4,CD=2,梯形ABCD的面积为6,∠ADC=60°,求平面α与底面ABCD所成锐二面角的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com