若函数f(x)满足:在定义域内存在实数x0,使f(x0+k)=f(x0)+f(k)(k为常数),则称“f(x)关于k可线性分解”.
(1)函数f(x)=2x+x2是否关于1可线性分解?请说明理由;
(2)已知函数g(x)=lnx-ax+1(a>0)关于a可线性分解,求a的范围;
(3)在(2)的条件下,当a取最小整数时;
(i)求g(x)的单调区间;
(ii)证明不等式:(n!)2≤en(n-1)(n∈N*).
(1)解:函数f(x)=2
x+x
2是关于1可线性分解,理由如下:
令h(x)=f(x+1)-f(x)-f(1)=2
x+1+(x+1)
2-2
x-x
2-2-1=2(2
x-1+x-1)
∴h(0)=-1<0,h(1)=2
∴h(x)在(0,1)上至少有一个零点
即存在x
0∈(0,1),使f(x
0+1)=f(x
0)+f(1);
(2)由已知,存在实数x
0,使g(x
0+a)=g(x
0)+g(a)(a为常数),
即ln(x
0+a)-a(x
0+a)+1=lnx
0-ax
0+1+lnx-a
2+1
∴
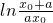
=1
∴
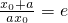
∴x
0=
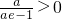
∵a>0,∴
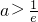
;
(3)(i)解:由(2)知,a=1,g(x)=lnx-x+1,
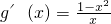
(x>0)
∴x∈(0,1)时,g′(x)>0,∴g(x)的增区间是(0,1);x∈(1,+∞)时,g′(x)<0,∴g(x)的减区间是(1,+∞);
(ii)证明:由(i)知x∈(0,+∞),g(x)≤g(1),即lnx-x+1≤0,∴lnx≤x-1
∴ln1=0,ln2<1,ln3<2,…,lnn<n-1
相加得:ln1+ln2+…+lnn≤1+2…+(n-1)
即lnn!≤

∴(n!)
2≤e
n(n-1)(当且仅当n=1时取“=”号).
分析:(1)函数f(x)=2
x+x
2是关于1可线性分解,令h(x)=f(x+1)-f(x)-f(1)=2(2
x-1+x-1),可得h(0)=-1<0,h(1)=2,利用零点存在定理,即可求得结论;
(2)根据新定义,可得ln(x
0+a)-a(x
0+a)+1=lnx
0-ax
0+1+lnx-a
2+1,从而可得x
0=
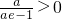
,由此可求a的范围;
(3)(i)求导函数,由导数的正负,即可求得g(x)的单调区间;
(ii)先证明lnx≤x-1,再累加,即可证得结论.
点评:本题考查新定义,考查学生的计算能力,解题的关键是正确理解新定义,属于中档题.

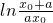 =1
=1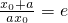
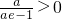
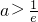 ;
;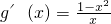 (x>0)
(x>0)
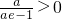 ,由此可求a的范围;
,由此可求a的范围;
