[题目]已知Rt△ABC的周长为定值l.则它的面积最大值为．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知Rt△ABC的周长为定值l，则它的面积最大值为．

【答案】
【解析】解：设三边为a，b，c，c为斜边，则c2=a2+b2．

∵a+b+c=1，

∴a2+b2=（1﹣a﹣b）2，化为：

1﹣2a﹣2b+2ab=0，

∴1+2ab=2（a+b）≥4 ，化为： ﹣4 +1≥0，解得 ≥ ，（舍去），

或 ≤ ，即ab≤ = ．当且仅当a=b= 时取等号．

∴它的面积最大值= ab= ．

故答案为：．

设三边法不为a，b，c，c为斜边，则c2=a2+b2．由a+b+c=1，可得a2+b2=（1﹣a﹣b）2，化为：1﹣2a﹣2b+2ab=0，变形1+2ab=2（a+b），再利用基本不等式的性质与三角形面积计算公式即可得出．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f（x）=x2+ax+b（a，b∈R）．（Ⅰ）已知x∈[0，1]
（i）若a=b=1，求函数f（x）的值域；
（ii）若函数f（x）的值域为[0，1]，求a，b的值；
（Ⅱ）当|x|≥2时，恒有f（x）≥0，且f（x）在区间（2，3]上的最大值为1，求a2+b2的最大值和最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，已知位于y轴左侧的圆C与y轴相切于点（0，1）且被x轴分成的两段圆弧长之比为1：2，过点H（0，t）的直线l于圆C相交于M、N两点，且以MN为直径的圆恰好经过坐标原点O．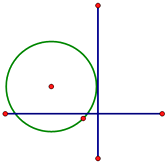

（1）求圆C的方程；
（2）当t=1时，求出直线l的方程；
（3）求直线OM的斜率k的取值范围．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知曲线x2+y=8与x轴交于A，B两点，动点P与A，B连线的斜率之积为．
（1）求动点P的轨迹C的方程．
（2）MN是动点P轨迹C的一条弦，且直线OM，ON的斜率之积为．求的最小值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设不等式组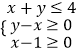，表示的平面区域为D，若圆C：（x+1）2+（y+1）2=r2（r＞0）经过区域D上的点，则r的取值范围是（）
A.[2 ，2 ]
B.（2 ，3 ]??
C.（3 ，2 ]
D.（0，2 ）∪（2 ，+∞）

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】设数列{an}是首项为0的递增数列，fn（x）=|sin （x﹣an）|，x∈[an ， an+1]，n∈N* ，满足：对于任意的b∈[0，1），fn（x）=b总有两个不同的根，则{an}的通项公式为

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某城市100户居民的月平均用电量（单位：度），以[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300）分组的频率分布直方图如图．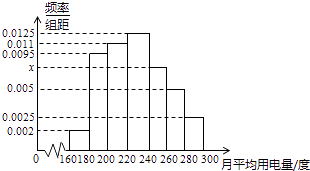

（1）求直方图中x的值；
（2）求月平均用电量的众数和中位数；
（3）在月平均用电量为，[220，240），[240，260），[260，280），[280，300）的四组用户中，用分层抽样的方法抽取11户居民，则月平均用电量在[220，240）的用户中应抽取多少户？

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】某毕业生参加人才招聘会，分别向甲、乙、丙三个公司投递了个人简历，假定该毕业生得到甲公司面试的概率为，得到乙公司和丙公司面试的概率均为p，且三个公司是否让其面试是相互独立的．记ξ为该毕业生得到面试的公司个数，若P（ξ=0）=
（Ⅰ）求p的值：
（Ⅱ）求随机变量ξ的分布列及数学期望．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知椭圆C： =1（a＞b＞0）的离心率为，且经过点A（0，﹣1）．
（1）求椭圆C的标准方程；
（2）如果过点的直线与椭圆交于M，N两点（M，N点与A点不重合），求证：△AMN为直角三角形．

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学