
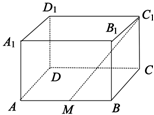
 如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.
如图,长方体ABCD-A1B1C1D1中,AB=2,BC=$\sqrt{2}$,CC1=1,M为线段AB的中点.分析 (1)说明∠MC1C就是异面直线DD1 与MC1所成的角,连接MC,在△C1MC中求解即可.
(2)连接BC1,说明∠MC1B为直线MC1与平面BB1C1C所成的角,由△MC1B为Rt△.求解即可.
(3)利用等体积转化,即可求三棱锥C-MC1D1的体积.
解答 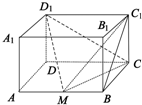 解:(1)因为C1C∥D1D,
解:(1)因为C1C∥D1D,
所以∠MC1C就是异面直线DD1 与MC1所成的角,…(2分)
连接MC,则△C1MC为Rt△,得MC=$\sqrt{3}$,MC1=2,
所以∠MC1C=60○.
即异面直线DD1 与MC1所成的角为60°;…(4分)
(2)因为MB⊥平面B1C1CB,连接BC1,则∠MC1B为直线MC1与平面BB1C1C所成的角,…(6分)
由△MC1B为Rt△,得BC1=$\sqrt{3}$,MC1=2,所以∠MC1B=30○,
即直线MC1与平面BB1C1C所成的角为300;…(8分)
(3)${V_{C-M{C_1}{D_1}}}={V_{M-C{C_1}{D_1}}}=\frac{1}{3}×{S_{△C{C_1}{D_1}}}×BC=\frac{1}{3}×\frac{1}{2}×1×2×\sqrt{2}=\frac{{\sqrt{2}}}{3}$.…..(12分)
点评 本题考查直线与平面所成角,异面直线所成角的求法,考查三棱锥体积的计算,考查空间想象能力以及计算能力.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 喜欢足球 | 不喜欢足球 | 总计 | |
| 男 | 35 | 15 | 50 |
| 女 | 25 | 25 | 50 |
| 总计 | 60 | 40 | 100 |
| P(K2≥k0) | 0.05 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
| A. | 有95%的把握认为“喜欢足球与性别相关” | |
| B. | 有95%的把握认为“喜欢足球与性别无关” | |
| C. | 在犯错误的概率不超过2.5%的前提下,认为“喜欢足球与性别无关” | |
| D. | 在犯错误的概率不超过2.5%的前提下,认为“喜欢足球与性别有关” |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 几何题 | 代数题 | 总计 | |
| 男同学 | 22 | 8 | 30 |
| 女同学 | 8 | 12 | 20 |
| 总计 | 30 | 20 | 50 |
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com