
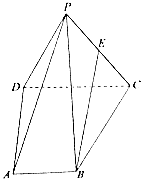
 如图所示,四棱锥P-ABCD的底面为直角梯形,AB⊥AD,CD⊥AD,CD=2AB.点E是PC的中点.
如图所示,四棱锥P-ABCD的底面为直角梯形,AB⊥AD,CD⊥AD,CD=2AB.点E是PC的中点.分析 (1)根据线面平行的判定定理即可证明:BE∥平面PAD;
(2)棱PD上存在点F为PD的中点,使CF⊥PA,利用三垂线定理可得结论.
解答 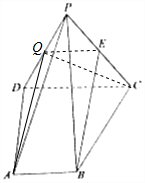 (1)证明:取PD中点Q,连结AQ、EQ.…(1分)
(1)证明:取PD中点Q,连结AQ、EQ.…(1分)
∵E为PC的中点,
∴EQ∥CD且EQ=$\frac{1}{2}$CD.…(2分)
又∵AB∥CD且AB=$\frac{1}{2}$CD,
∴EQ∥AB且EQ=AB.…(3分)
∴四边形ABED是平行四边形,
∴BE∥AQ.…(4分)
又∵BE?平面PAD,AQ?平面PAD,
∴BE∥平面PAD.…(5分)
(2)解:棱PD上存在点F为PD的中点,使CF⊥PA,
∵平面PCD⊥底面ABCD,平面PCD∩底面ABCD=CD,AD⊥CD,
∴AD⊥平面PCD,
∴DP是PA在平面PCD中的射影,
∴PC=DC,PF=DF,
∴CF⊥DP,
∴CF⊥PA.
点评 本题主要考查空间直线和平面平行或垂直的判断,要求熟练掌握相应的判定定理.考查学生的推理能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | -$\frac{6}{5}$ | B. | $\frac{6}{5}$ | C. | $\frac{9}{10}$ | D. | -$\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
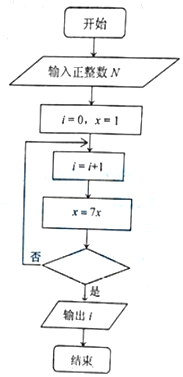 某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )
某同学为实现“给定正整数N,求最小的正整数i,使得7i>N,”设计程序框图如右,则判断框中可填入( )| A. | x≤N | B. | x<N | C. | x>N | D. | x≥N |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2017}$,+∞) | B. | (-2017,+∞) | C. | (-$\frac{2}{3}$,+∞) | D. | (-2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).
在某校举行的航天知识竞赛中,参与竞赛的文科生与理科生人数之比为1:3,且成绩分布在[40,100],分数在80以上(含80)的同学获奖.按文理科用分层抽样的方法抽取200人的成绩作为样本,得到成绩的频率分布直方图(见图).| 文科生 | 理科生 | 合计 | |
| 获奖 | 5 | ||
| 不获奖 | |||
| 合计 | 200 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,$\frac{1}{5}$] | B. | [-$\frac{1}{5}$,1] | C. | (-$\frac{1}{5}$,$\frac{1}{3}$] | D. | ($\frac{1}{3}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y<xz | B. | x<z<y | C. | z<y<x | D. | x<y<z |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com