
分析 根据题意,点Q到三个侧面的垂线与侧棱PA、PB、PC围成一个棱长为3$\sqrt{2}$、4$\sqrt{2}$、5$\sqrt{2}$的长方体,分析可知以PQ为直径的球是它的外接球,再由长方体和其外接球的关系求解.
解答 解:根据题意:点Q到三个侧面的垂线与侧棱PA、PB、PC围成一个棱长为3$\sqrt{2}$、4$\sqrt{2}$、5$\sqrt{2}$的长方体,
则其外接球的直径即为PQ且为长方体的体对角线.
2R=$\sqrt{(3\sqrt{2})^{2}+(4\sqrt{2})^{2}+(5\sqrt{2})^{2}}=10$.
由球的体积公式得V=$\frac{4}{3}π{R}^{3}=\frac{500}{3}π$
故答案为:$\frac{500}{3}π$.
点评 本题主要考查空间几何体的构造和组合体的基本关系,确定外接球的直径即为PQ且为长方体的体对角线是关键.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±4 | B. | ±2$\sqrt{5}$ | C. | ±2$\sqrt{6}$ | D. | ±5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
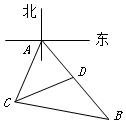 为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.
为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com